示例:有理函数回归 2
rationalfitnp - 无极点
使用 rationalfit 和 rationalfitnp 函数执行有理函数回归。当您使用 rationalfitnp 函数替代 rationalfit 函数时,将在拟合区间中检查传统最小二乘问题的解是否为分母的根。如果没有极点,则返回所生成的拟合。如果有极点,则向非线性最优化问题添加附加约束。
1. 通过对 x 的反函数稍作修改来定义数据集。
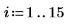
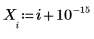
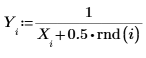
2. 指定有理函数分子和分母的阶数。
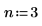
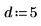
拟合函数具有下列形式:
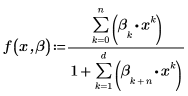
3. 定义置信限及标准差矢量。
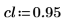
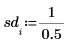
4. 调用 rationalfit 和 rationalfitnp 函数。
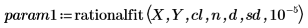 | 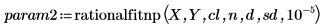 |
 |  |
对于 param1 和 param2,第一列包含参数,而其余列包含针对上面所定义的置信限每个参数的上下边界。
5. 绘制数据集图像及两回归曲线。
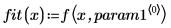
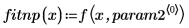
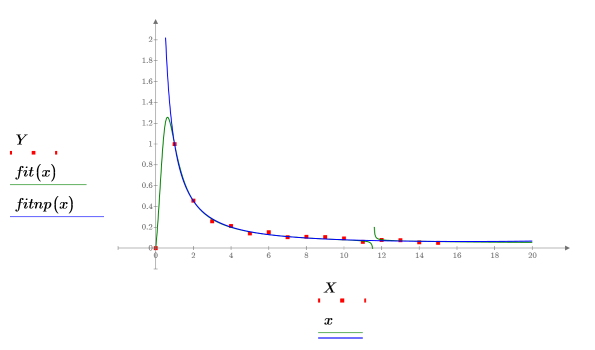
通过 rationalfitnp 函数移除极点。其分母多项式的体现形式如下:
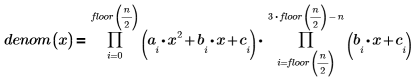
要避免出现极点,可添加下列约束:
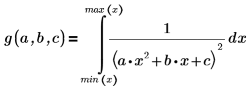
 | 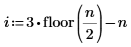 |
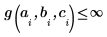 | 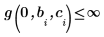 |
LeastSquaresFit
对比 rationalfitnp 和 LeastSquaresFit 所返回的拟合曲线。LeastSquaresFit 函数所执行的算法与 rationalfitnp 的相同,但其需要参数的估值及置信限。当您想使常数项位于分子而非分母中时,您可能希望进行此操作。
1. 定义拟合函数。
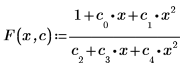
2. 定义参数的估值。
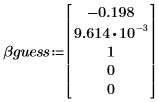
3. 定义参数的上下边界条件。

4. 调用 LeastSquaresFit 函数。
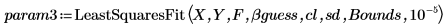
5. 绘制数据集图像,以及 rationalfitnp 和 LeastSquaresFit 函数所返回的拟合曲线。
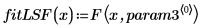
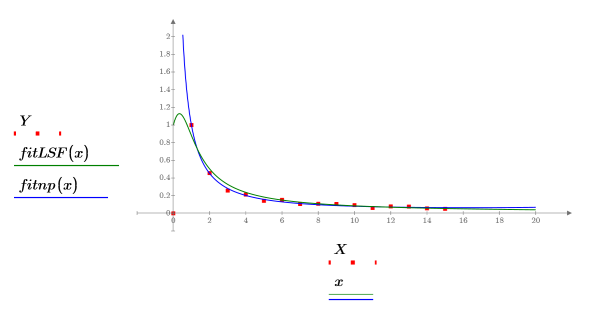
任何在进行有理函数拟合之前使数据偏向直线的滤波或数据变换方法都将很大程度地加快 rational 函数的收敛速度,并可能收到去除不必要极点的额外益处。 |