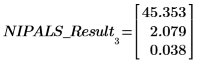示例:主分量分析 1
Nipals 函数
1. 定义一个数据集,其中每列代表一个变量。


2. 绘制数据集图像。
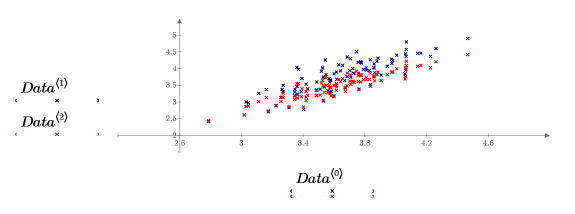
在此图表中,x-y 平面和 x-z 平面叠加,以显示数据中的趋势。该数据实际上是椭圆形的点云,它们几乎都位于一个平面上。三个变量线性相关,与理想平面的偏差是由噪声导致的。
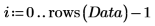
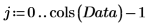
4. 为了将数据中心化,先使用均值函数求出数据均值,然后从各变量中减去该均值。
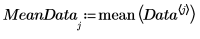
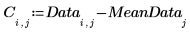
5. 绘制中心化数据。
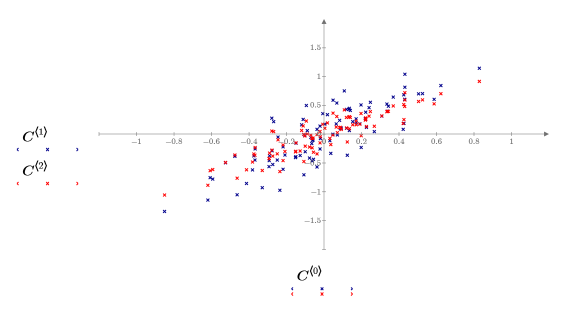
• 数据现在相对于原点居中。本步骤是 Nipals 函数自动执行的步骤之一。 • 在许多 PCA 应用中,某些情况下 (例如不同变量的单位不同时) 还需要对数据进行换算,以使变量的权重相等。通常情况下是将各变量 (“数据”的各列) 换算为单位方差,但这种方法对此数据并不适合,因此这里未进行换算。 |
6. 使用 Nipals 函数创建新变量空间。使用三个主分量 (这是最大的可能,因为只有三个变量可以作为起始点)。
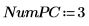
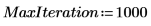
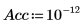
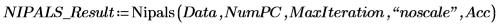
Nipals 函数的输出是一个由六个单独矩阵组成的嵌套矩阵。使用它求出数据的 loadings、scores、eigenvals 和 eigenvecs。如有需要,使用 Nipals2 函数和最后两个矩阵来提取附加分量。
输入和分数
1. 调用 loadings 函数来检索在 NIPALS_Result 的第二个矩阵中找到的数据。
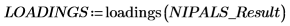
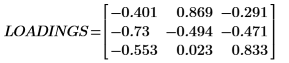
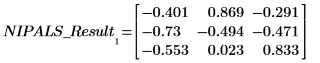
LOADINGS 的各列为输入矢量。
2. 调用 scores 函数来检索在 NIPALS_Result 的第一个矩阵中找到的数据。
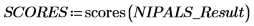

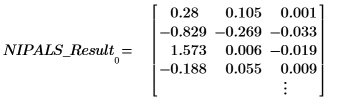
分数代表重建原始谱时要添加的输入矢量的比例。将它们视为强度。数据 = LOADINGS * SCOREST。
3. 绘制 SCORES 矩阵中存储的数据。
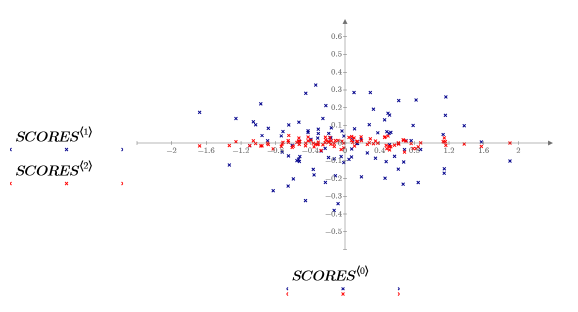
已将数据旋转,以便第一变量可以对最大方差量加以解释。这在椭圆形点云的长轴上有所显示,此轴现在平行于 x 轴。第三个变量 (平行于 z 轴) 的值很小。大多数情况下,可以舍弃此变量。您已完成数据的压缩。
PCA 方差和特征值
1. 使用 PCAvariance 函数返回三个主分量的累积方差。
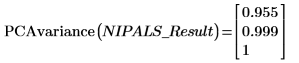
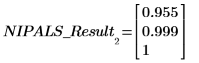
前两个分量构成系统中 99.9% 的方差。
2. 使用 PCAeigenvals 函数提取主分量的特征值。