示例:非线性回归 2
使用 LeastSquaresFit 函数执行非线性回归。LeastSquaresFit 求解器为求解非线性回归问题提供了最大灵活性。利用该求解器,您可以输入任意相关参数的约束方程、参数的上下界、x 值的标准差,以及计算的置信限。
LeastSquaresFit
1. 定义数据集。
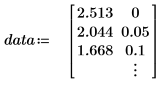
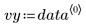
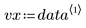
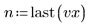
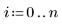
该数据取自 NIST 网站上介绍的示例。使用下列方程生成 14 位精度的数据:
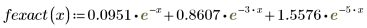
2. 定义拟合函数。
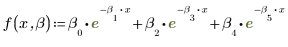
以上各个参数是矢量 β 的元素。您还可以利用各变量名代替矢量的元素来指定输入函数:
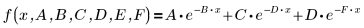
3. 提供估值。
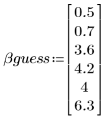
4. 定义参数置信限。
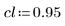
5. 调用 LeastSquaresFit 函数。
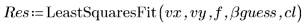
该求解器采用序列二次规划法 (SQP) 求解产生的最小二乘问题。通过引入附加变量,可将原始问题变换为常规等式约束的非线性规划问题。一般说来,这种方法较之其他方法更加快速和稳定。
6. 查看 LeastSquaresFit 函数所返回的输出矢量。
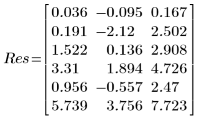
◦ 输出的第一列包含拟合参数的值。第二列和第三列分别包含参数置信区间的左、右边界。
◦ 95% 的参数置信限覆盖了相当广的值域,这表示拟合困难,而且各参数可能差别很大。因此,拟合参数的值不同于 NIST 网站所记录的正确值:
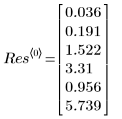

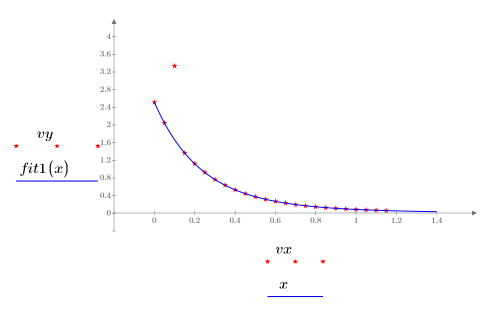
7. 绘制数据、最小二乘拟合以及 NIST 拟合的图像。
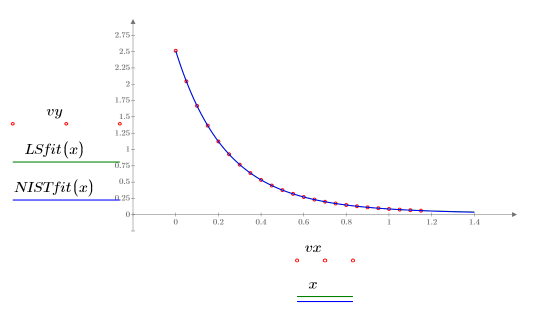
8. 将最小二乘拟合与原始数据进行对比:
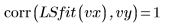
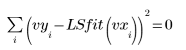
拟合逼近收敛,但这可能得益于收敛公差的调整。这可通过 LeastSquaresFit 函数的一个可选自变量来完成。
约束、标准差和公差
LeastSquaresFit 有数个可选自变量:
• 标准差矢量
• 下界和上界矩阵
• 精度
您可以单独使用这些可选自变量中的任何一个,但如果输入多于一个自变量,需要考虑自变量的顺序。
1. 干扰其中一个数据值来模拟测量不准的值。
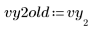
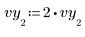
2. 指定上下界以对拟合值进行约束。
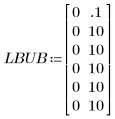
将边界完全设置于期望参数值之外,这是由于在此例中没有已知的特定边界。
3. 设置每个 y 值的标准差矢量以屏蔽离群值。
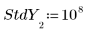
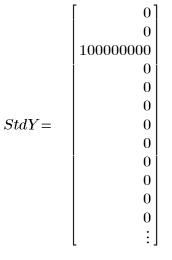
◦ 较大的标准差值 108 可有效地从计算中移除测量不准的值。
◦ 当输入标准差矢量作为 LeastSquaresFit 函数的自变量时,求解器会最小化下列函数
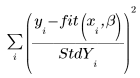
如果某个点的标准差为 0,则在该点使用原始的无偏差函数,即,StdYi 设置为 1。
4. 设置精度以将更严格的收敛公差应用于计算 (默认值为 10-7)。
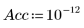
5. 调用使用和不使用标准差的 LeastSquaresFit 函数。
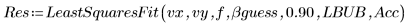
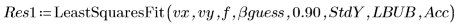
◦ 未进行屏蔽的计算失败是由于置信限过大。
◦ 新的参数更接近 NIST 值:
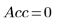
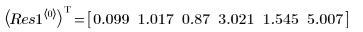
6. 使用异常值和屏蔽拟合绘制数据。
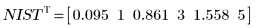
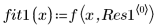
参考文献
此示例的数据源自 Lanczos, C., Applied Analysis, Prentice Hall, 1956,第 272-280 页的 NIST Statistical Reference Dataset Archive。