示例:LU 矩阵因式分解
使用 LU 函数执行 LU 矩阵因式分解。
|
|
要在进行布尔值比较时避免逻辑不匹配,请在计算选项下拉列表中启用约等。
|
实矩阵的 LU 因式分解
1. 定义一个 m x n 维的实数矩阵 M1,使 m > n。
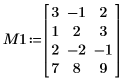
2. 使用 LU 函数对矩阵 M1 执行 LU 矩阵因式分解。

3. 显示 P1 x M1 = L1 x U1。
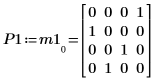 |  | 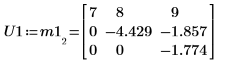 |
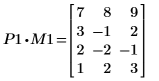 | 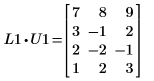 | |
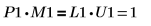 |
该关系在逻辑上是正确的。
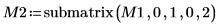 |
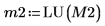 |
5. 显示 P2 x M2 = L2 x U2。
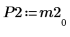 | 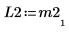 | 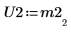 |
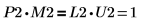 |
该关系在逻辑上是正确的。
6. 使用函数 submatrix 提取矩阵 M3,使 m = n。
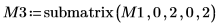 |
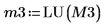 |
7. 显示 P3 x M3 = L3 x U3。
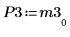 | 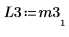 | 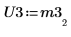 |
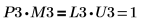 |
该关系在逻辑上是正确的。
复数矩阵的 LU 因式分解
1. 定义一个 m x n 维的复数矩阵 C1,使 m > n。
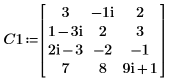
2. 使用 LU 函数对矩阵 C1 执行 LU 矩阵因式分解。

3. 显示 P4 x C1 = L4 x U4。
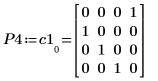 | 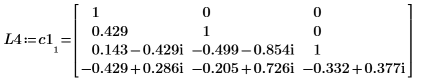 | 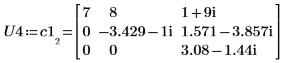 |
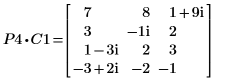 | 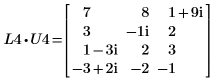 | |
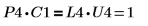 |
该关系在逻辑上是正确的。
4. 使用函数 submatrix 提取矩阵 C2,使 m < n。
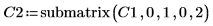 | 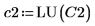 | 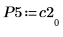 |
5. 显示 P5 x C2 = L5 x U5。
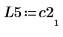 | 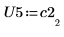 |
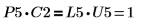 |
该关系在逻辑上是正确的。
6. 使用函数 submatrix 提取矩阵 C3,使 m = n。
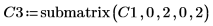
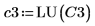
7. 显示 P6 x C3 = L6 x U6。
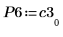 | 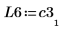 | 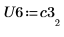 |
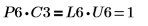 |
该关系在逻辑上是正确的。