示例:线性预测法
使用函数 burg 和 yulew 为已命名的线性预测模型生成系数。这些函数分别执行 Burg 方法和 Yule-Walker 算法。有关这些算法及其相关数学知识的说明,请参见 Macmillan 1989 年出版的 Sophocles J. Orfanidis 著的 Optimum Signal Processing (《最优信号处理》)。
Yule-Walker 预测
1. 使用 cos 函数来定义余弦信号。
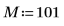
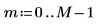
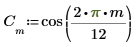
2. 绘制信号图像。
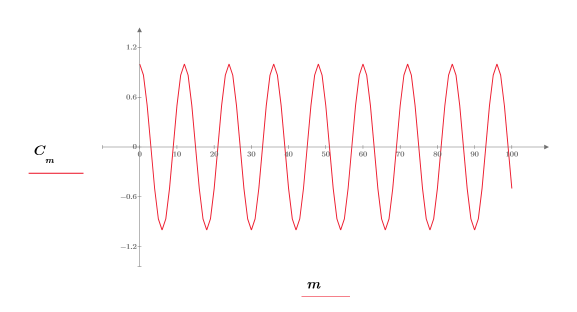
3. 使用 rnd 函数向信号添加随机噪声。
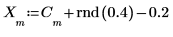
4. 绘制原始信号和噪声信号的图像。
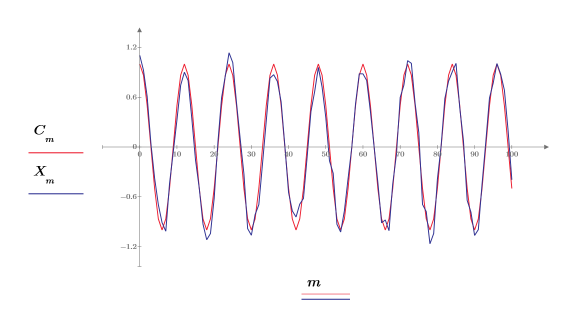
从信号中减去 0.2 以使随机分量的中心位于振幅 0 附近。
5. 从信号的起始位置获取时间较短的样本集。
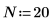
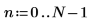
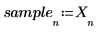
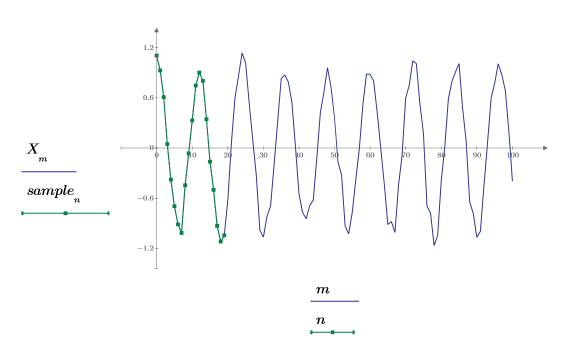
6. 设置预测阶数,并使用 yulew 函数来计算系数。
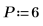
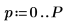

◦ 这些系数适用于与原始信号接近的所有极点滤波器。正如所预期的那样,存在一个表示余弦的大极点以及多个近似噪声的小极点。
◦ 阶数 P 可确定用于预测序列中下一个值的连续值的数量。将使用系数矢量中的第一个至第六个元素,并忽略始终为 1 的第零个元素。当将 y 用作预测误差滤波器以生成一组完整的预测误差时,将需要始终为 1 的第零个元素。
7. 将通过信号中前 P 个点计算所得的预测点与原始数据进行比较。这会显示被用来替换信号 X 时滤波器的性能如何。
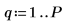
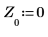
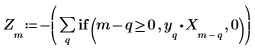
8. 绘制原始信号和预测信号的图像。
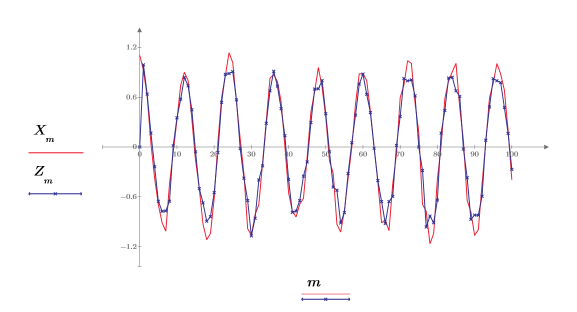
即使仅使用数据的前 20 个点,近似效果也非常理想。
9. 将系数数组用作滤波器,然后计算作为输入的样本的响应,以使用 response 函数来生成 Yule-Walker 系数的预测误差。
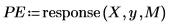
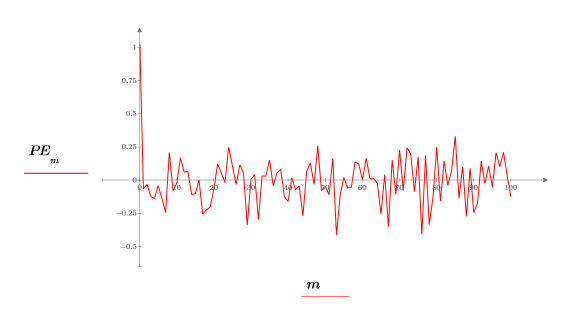
有时,也将完整的系数数组称为预测误差滤波器。
10. 验证这些误差是否确实能给出先前两个绘图之间的差异。
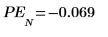
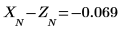
使用 Yule-Walker 算法求预测误差平方和的最小值。
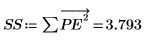
11. 通过施加干扰 y (向除第一个系数之外的其他所有系数添加小的随机量) 和重新计算总和 (将光标置于下面的 rnd 函数上并按几次 [F5] 键) 来对该最小化情况进行抽查。
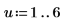
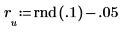
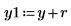
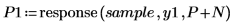
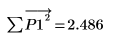
Burg 预测
1. 构建线性预测应正常工作的序列:带有已知系数的自回归过程。
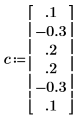
2. 初始化时间序列。
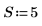
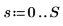
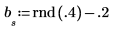
3. 通过使用自回归外加噪声来生成其余的时间序列。
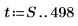
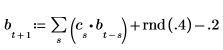
4. 将整个时间序列作为样本并计算阶数为 6 的模型的系数,然后使用 burg 函数来计算系数。
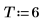
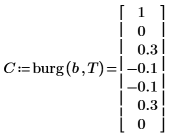
5. 使用本文档中的符号约定来比较实际生成过程的系数。
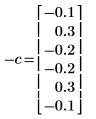
◦ 第零个系数已被忽略,因为它始终等于 1。
◦ 计算的 C 的元素 1 和 5 是不同的。
6. 使用 Burg 系数矢量 C 生成预测误差。
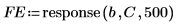
◦ Burg 方法为前 P 个误差分配零权重,因此最小化不会受到样本补零的影响,这如同使用 Yule-Walker 法进行最小化一样。
◦ Burg 标准还涉及前向误差 FE 以及后向误差 BE。
7. 使用 response 和 reverse 函数来计算后向误差。
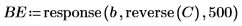
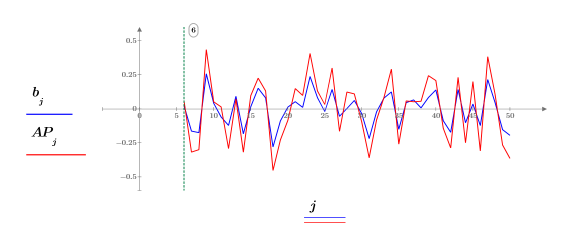
8. 使用预测误差 FE 和自回归函数 b 计算实际预测 AP,然后绘制从第 Pth 项开始的一段预测序列和实际序列。
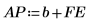
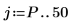
谱估计
可以使用由线性预测方法生成的系数来估计所建模过程的功率谱。在此环境中,Burg 算法称为最大熵谱分析 (MESA),在某些情况下,与 FFT 相比,该算法可更精确地确定短时间序列谱。
估计由添加了高斯噪声的正弦之和所组成的过程功率谱。
1. 使用 sin 函数来定义具有两个正弦分量的信号。
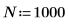
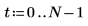
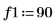
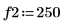
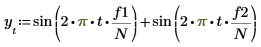
2. 使用 gaussn 函数来添加一些高斯噪声。
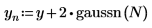
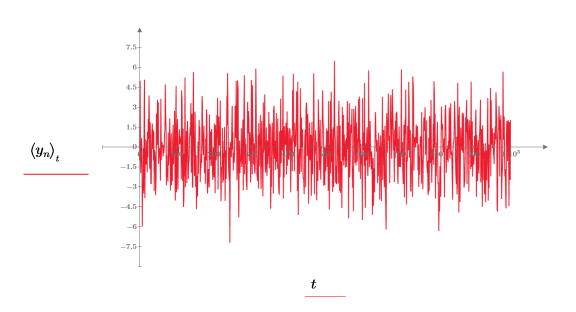
函数 gaussn 将返回随机数字的 n 元素矢量,这些随机数字符合均值为 0、标准差为 1 的高斯概率分布。
3. 定义线性预测的两个阶数。
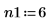
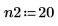
4. 以整个时间序列作为样本,使用 burg 函数来估算两阶自回归模型的频谱。
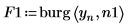
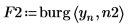
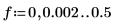
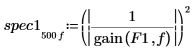
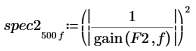
6. 绘制两个功率谱。
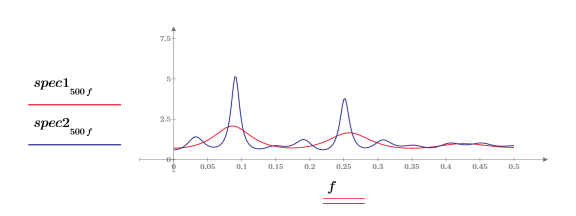
◦ 每个功率谱有两个峰值。
◦ 两个谱的较低和较高频率峰值出现的频率大致相同。
7. 将 spec1 和 spec2 曲线细分为两段,以便求出增益峰值及其发生的频率。
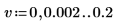 | 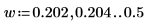 |
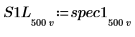 | 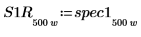 |
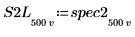 | 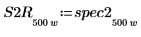 |
8. 使用 if 函数来定义一个函数,以返回给定线段出现峰值的频率,然后用其求出每个谱轨迹左侧和右侧的峰值。
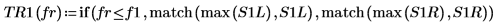 | |
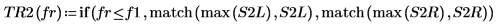 | |
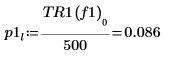 | 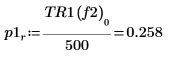 |
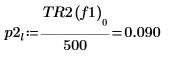 | 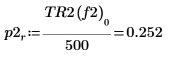 |
9. 使用 max 函数来计算每个峰值的幅度。
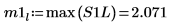 | 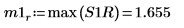 |
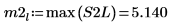 | 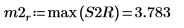 |
10. 分别绘制每个函数的图像。使用水平和竖直标记来显示每个峰值幅度及其出现的频率。
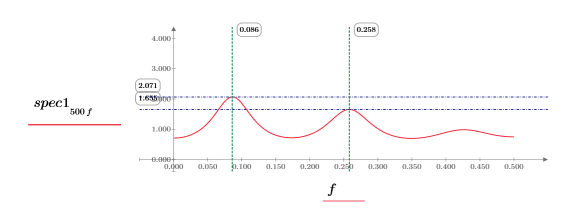
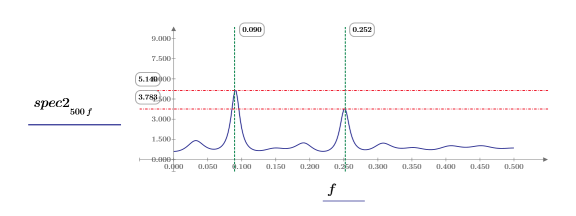
◦ 在重新计算工作表的同时查看这两个绘图。
◦ 峰值的幅度会随着每次重新计算而有所变化,它们通常具有不同的值。但是,幅度可能会相等。
◦ 峰值出现的频率大致相同。
有关这种谱估计方法的详细信息,请参阅由 S. Lawrence Marple, Jr. (Prentice Hall,Inc) 编著的 Digital Spectral Analysis with Applications (《应用程序数字频谱分析》)。