示例:开尔文函数
1. 绘制 0th 阶函数 ber 和 bei:
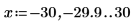

两个函数看似对称。
2. 重新设置刻度值来放大 x 轴以便显示函数 ber 和 bei 的两个峰值是如何随阶数增大而更改变化的:
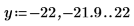
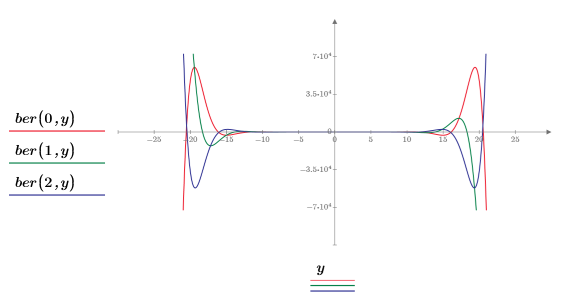
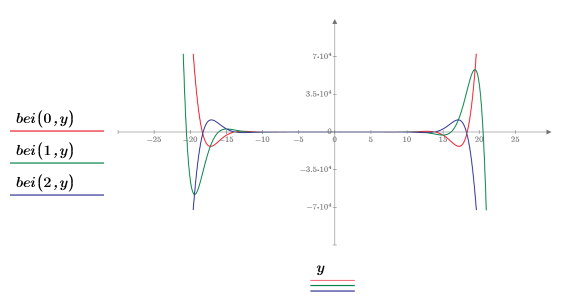
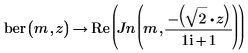
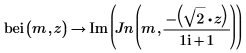
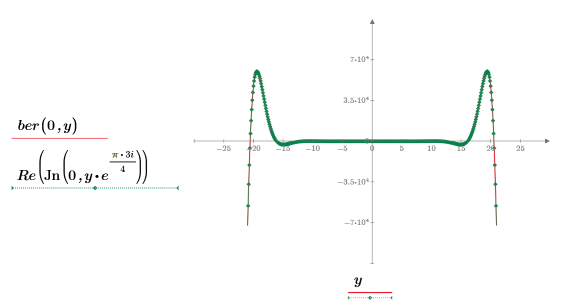
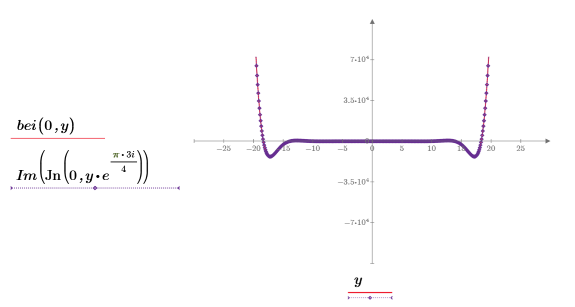
该示例重点在于 ber 函数,但同一观察值也可应用于函数 bei 中。
4. 用函数 ber 定义矢量 Z1:
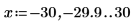
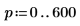
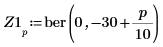
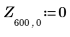
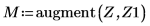
5. 求函数 ber 的局部极小值:

ber 函数在 m=0 时有 8 个极小值。该函数为对称函数。高阶函数具有不同数量的极小值,它们均有不同的位置和振幅。
6. 求函数 ber 的局部极大值:

ber 函数在 m=0 时有 7 个峰值。该函数为对称函数。高阶函数具有不同数量的极大值,他们均有不同的位置和振幅。
7. 求出右侧四个极小值的纵坐标。
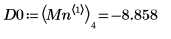
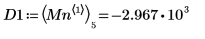
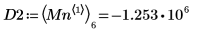
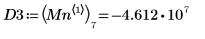
8. 使用函数 match 求出各匹配极小值的索引,然后求出对应的横坐标。
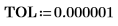
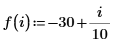
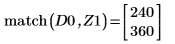
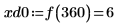
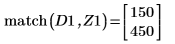
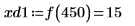
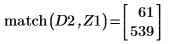
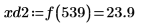
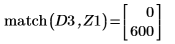
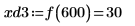
9. 找出右侧四个极大值的纵坐标。
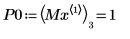
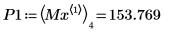
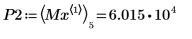
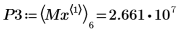
10. 使用函数 match 求出各匹配极大值的索引,然后求出对应的横坐标。
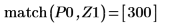
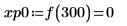
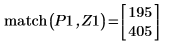
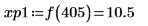
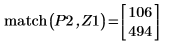
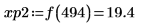
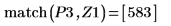
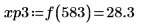
极大值和极小值振幅的范围变化很大,因此很难在一张图像中看到这些振幅的全部。 |
11. 使用标记来显示第一个极小值 (D0) 和第一个极大值 (P0):
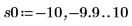
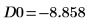
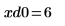
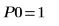
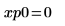
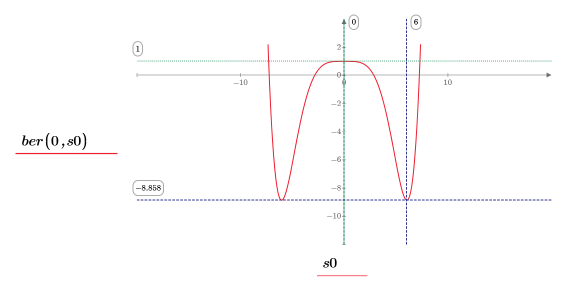
如预期的一样,图像会在 y 轴左侧显示第二个极小值。
12. 使用标记来显示下一个极小值 (D1) 和下一个极大值 (P1):
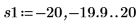
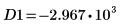
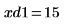
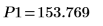
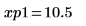
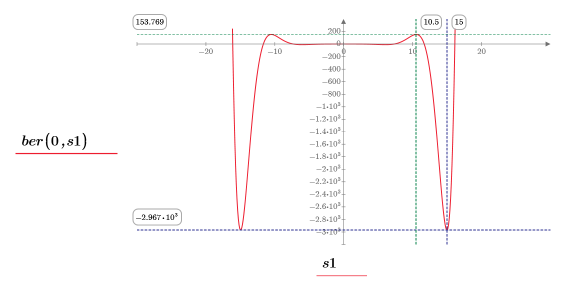
如预期的一样,图像会在 y 轴左侧显示第二个极小值和第二个极大值。
13. 使用标记来显示下一个极小值 (D2) 和下一个极大值 (P2):
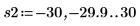
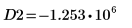
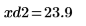
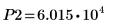
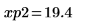
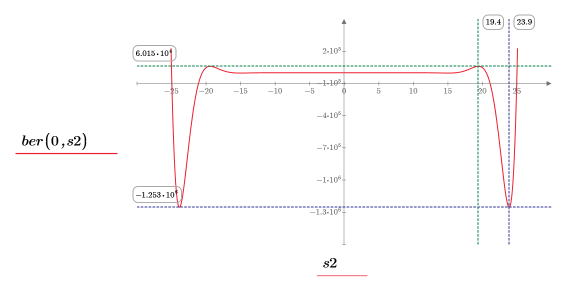
如预期的一样,图像会在 y 轴左侧显示第二个极小值和第二个极大值。
14. 使用标记来显示下一个极小值 (D3) 和下一个极大值 (P3):
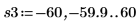
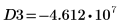
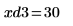
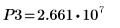
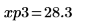
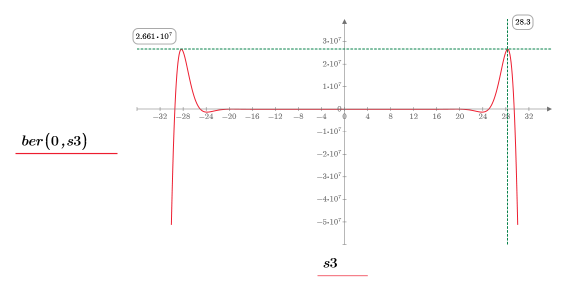
如预期的一样,图像会在 y 轴左侧显示第二个极大值。
极小值 (D3) 及其左侧的对应值,正好落在值域的边界处,因此最好将它们忽略。 |