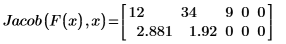示例:雅可比函数
使用 Jacob 函数计算矢量函数的 Jacobian,将其写为实数值函数的列矢量形式。
1. 定义包含在矢量 F 内的两个函数:
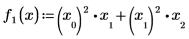
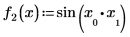
2. 定义矢量 F:
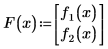
3. 由于未以数值形式对变量加以定义,以符号形式来计算 Jacob。
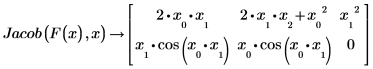
◦ 矩阵的 0 行包含三个元素:相对于 x0 的 f1 偏导数、相对于 x1 的偏导数和相对于 x2 的偏导数。
◦ 同样地,1 行包含三个元素:f2 对 x0 的偏导数、对 x1 的偏导数和对 x2 的偏导数。
PTC Mathcad 假定变量数等于 maxsub + 1,其中 maxsub 为出现在函数变量中的最大下标。 |
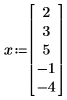
4. 给变量赋数值,之后以数值形式计算 Jacob 函数:
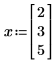
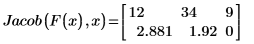
指定没有出现在函数中的附加变量
1. 通过设置 Jacob 可选的第三个自变量迫使结果矩阵包含多于变量数的列:
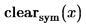
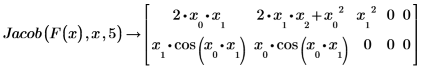
2. 通过为不存在的变量赋值迫使结果矩阵包含多于变量数的列: