示例:FFT 简介
快速傅立叶变换 (FFT) 是一种数值方法,表示一组随时间测量的数据的频谱。通常,数据是连续的,构成一个波形。要以数值形式使用数据,应以固定的时间间隔并以某一采样率对数据进行采样。下面各图给出了某些采样波形,以及针对频率绘制的傅立叶变换的幅度。
采样的正弦波形
1. 使用 sin 函数来定义正弦波形。
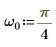
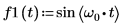
2. 设置数据点的数量。
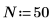
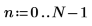
3. 设置样本间距。
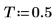
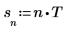
4. 设置采样率。
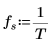
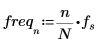
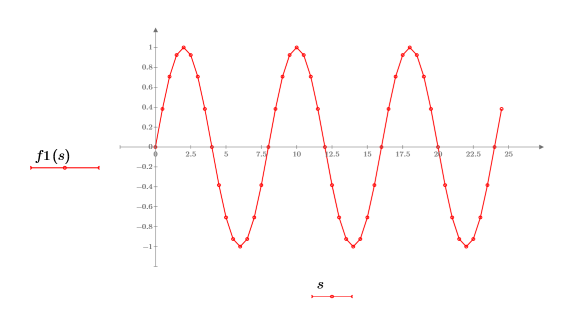
5. 对正弦函数绘图。
6. 使用 dft 函数计算离散傅立叶变换。
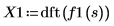
X1 为实数矢量和复数矢量。
7. 求出现峰值幅度时的频率。
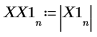
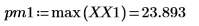
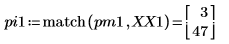
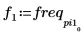
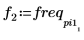
8. 绘制变换后的信号并使用标记显示各个峰值的频率和幅度。
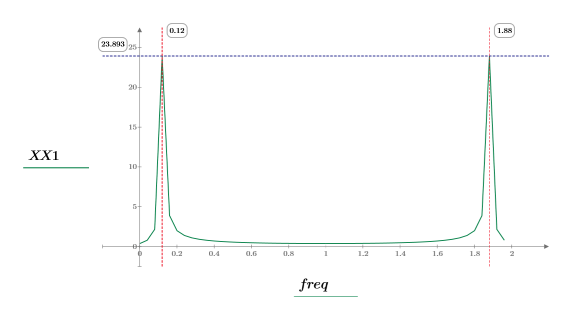
采样的余弦波形
1. 使用 cos 函数来定义余弦波形。
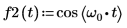
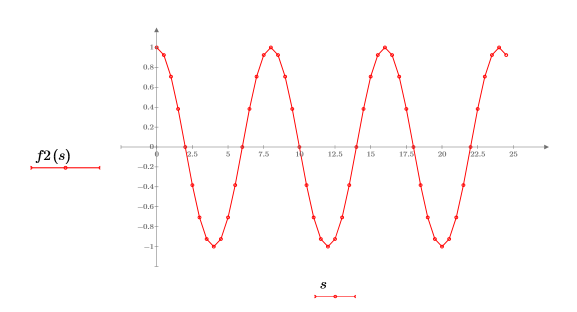
2. 绘制余弦函数的图像。
3. 使用 dft 函数计算离散傅立叶变换。
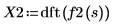
X2 为实数矢量和复数矢量。
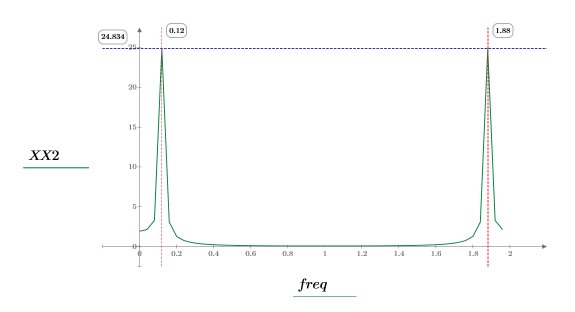
4. 求出现最大幅度时的频率。
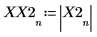
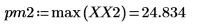
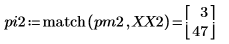
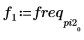
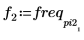
5. 绘制变换后的信号并使用标记显示各个峰值的频率和幅度。
采样的指数曲线波形
1. 使用 exp 函数来定义指数波形。
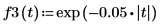
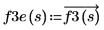
由于定义内的行列式运算符返回的是单个标量值,因此使用矢量化运算符来获得逐个元素的函数值。
2. 绘制指数函数图像。
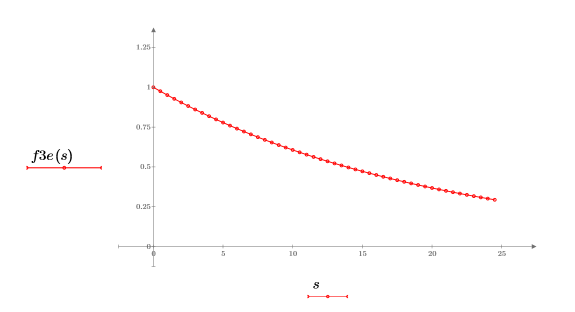
3. 使用 dft 函数计算离散傅立叶变换。
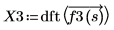
X3 为实数矢量和复数矢量。
4. 求出现最大幅度时的频率。
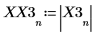
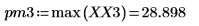
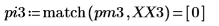
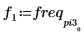
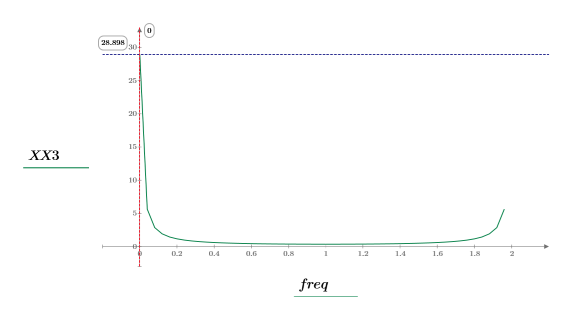
5. 绘制变换后的信号并使用标记显示各个峰值的频率和幅度。
采样阶跃波形
1. 使用 if 函数来定义阶跃波形。
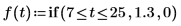
2. 计算每个区间的脉冲幅度。
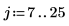
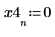
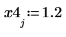
3. 绘制阶跃函数的图像。
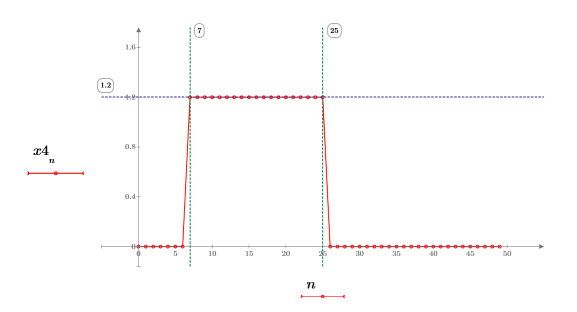
幅度在 7 到 25 之间一律为 1.2。
4. 使用 dft 函数计算离散傅立叶变换。
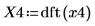
X4 为实数矢量和复数矢量。
5. 求出现最大幅度时的频率。
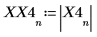
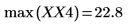
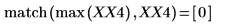
6. 绘制变换后的信号并使用标记显示各个峰值的频率和幅度。
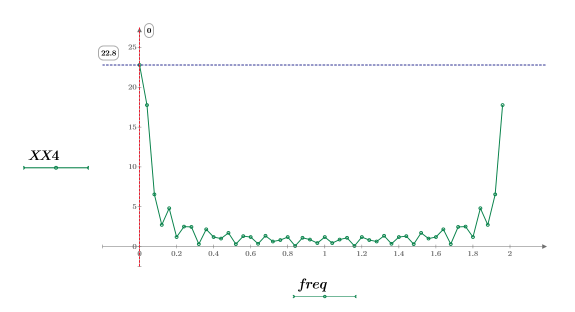
最大幅度出现在 freq0 处。