示例:以元素为单位的相位
函数 phasecor 将表示相位信息的实矢量作为自变量,然后在必要时依次将该矢量的各个元素加上 2p 的倍数 (保持数据的完整性),以产生连续的数据集。
四元素矢量
1. 定义简单复矢量。
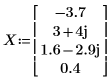
2. 使用函数 phase 查找以元素为单位的相位。
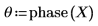
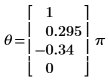
通常情况下,相位计算逐个元素进行,与过往的相位历史无关。这样,当穿过负实轴时,由于角度从 +p 变为了 -p,会导致结果相位数据中产生极大的跳跃不连续性。
3. 定义另一复矢量。
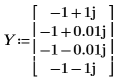
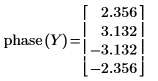
结果相位的第二和第三元素之间出现了极大的跳跃不连续性。
4. 应用 phasecor 函数以消除这种不连续性。
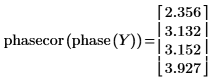
噪声信号
1. 定义信号参数。
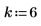
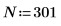
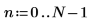
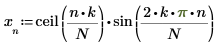
3. 3. 使用函数 whiten 添加白噪声,然后绘制结果信号。
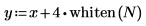
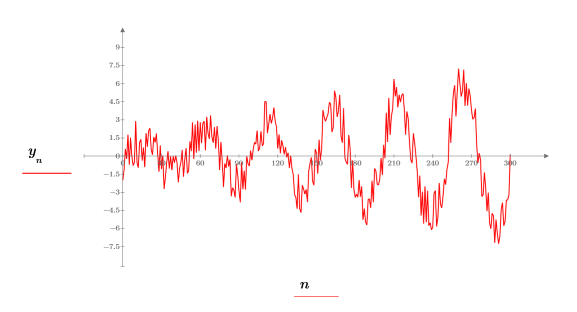
4. 使用函数 dft 计算样本信号的傅立叶变换。
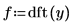
5. 将 phase 函数应用于样本信号的傅立叶变换。
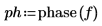
6. 绘制相位信号。
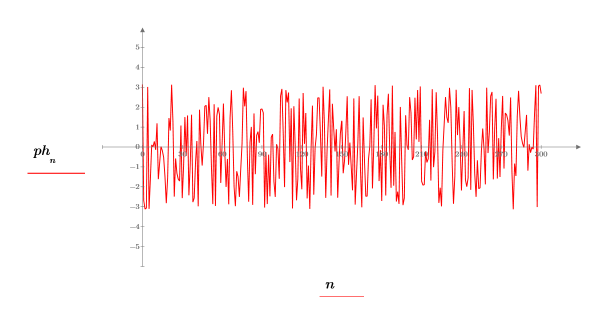
7. 使用函数 phasecor 将相位修正为连续信号,然后绘制结果输出。
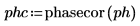
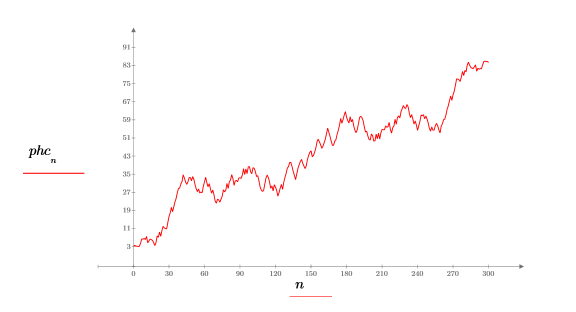
如果相位变化过快,phasecor 函数可能会失效。
8. 设置分频 f0 的值,然后绘制 phase 和 phasecor 的输出。
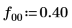
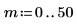
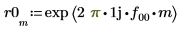
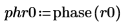
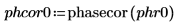
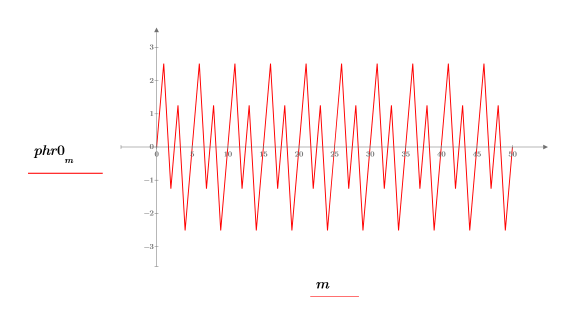
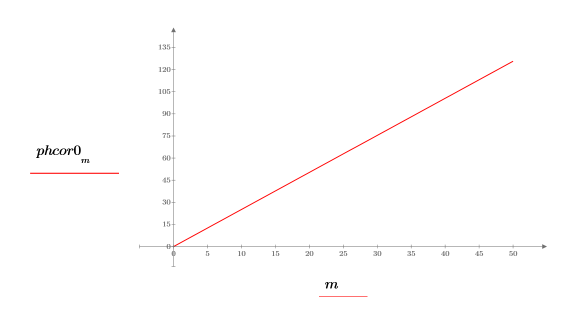
9. 计算分频 f0 值为 0.45、0.50 和 0.55 时的 phase 和 phasecor 的输出。
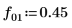 | 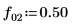 | 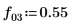 |
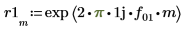 | 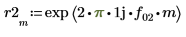 | 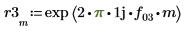 |
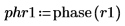 | 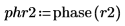 | 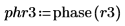 |
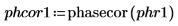 | 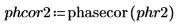 | 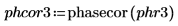 |
10. 在单个绘图上绘制相位函数的输出。
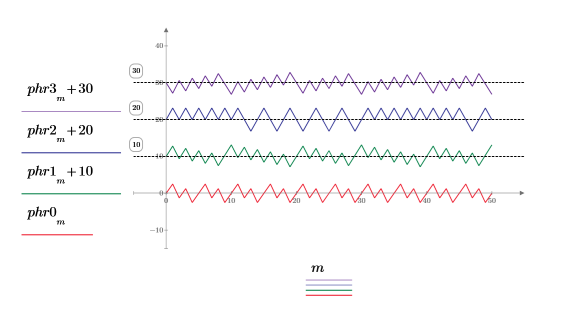
这些轨迹在 y 轴方向上不自然地变换,以显示每个频率的相位轨迹。
11. 在单个绘图上绘制函数 phasecor 的输出。
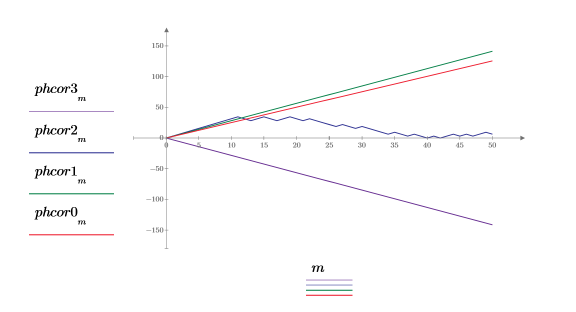
随着分频从 0.40 增大至 0.45 乃至 0.50,phasecor 的输出在正方向的斜率也将增大,当分频设为 0.55 时,输出变为负值。请参阅上一个相位图。