示例:特征矢量和特征值
使用 eigenvals、eigenvecs 和 eigenvec 函数可求出实数 (或复数) 矩阵的特征值和特征矢量。理论上,对于矩阵 M,如果您能找到满足以下条件的数字 λ,则非零矢量 v 即为 M 的特征矢量:
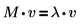
1. 定义输入方阵。
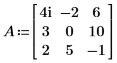
2. 调用 eigenvals 和 eigenvecs 以求出矩阵 A 的特征值和特征矢量。
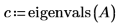
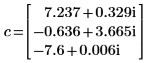
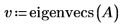

v 中第一列是与 c 中第一个元素相对应的特征矢量。类似地,v 中第二列是与 c 中第二个元素对应的特征矢量,依次类推。
3. 将 v1 定义为第一个特征矢量并将 c1 定义为 A 的第一个特征值。比较 A x v1 和 c1 x v1。
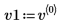
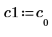
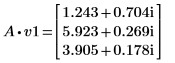 | 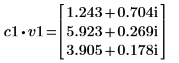 |
4. 将 v2 定义为第一个特征矢量并将 c2 定义为 A 的第一个特征值。比较 A x v2 和 c2 x v2。
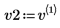
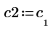
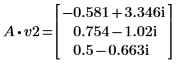 | 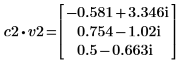 |
5. 将 v3 定义为第一个特征矢量并将 c3 定义为 A 的第一个特征值。比较 A x v3 和 c3 x v3。
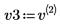
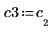
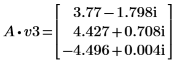 | 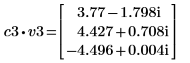 |
6. 调用 eigenvec 函数以返回特定特征值的单一特征矢量。
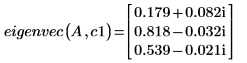

eigenvec 和 eigenvecs 所返回的结果并不一定匹配,然而它们都是有效解。特征矢量不是唯一的。它通过比例因子与其他特征矢量相关。对于一个给定的特征值,有无数个特征矢量。