示例:柯西分布
1. 显示柯西分布的定义:
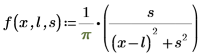
其中:
◦ l 是位置参数 (均值)
◦ s 是尺度参数 (方差的平方根),s > 0
2. 定义位置参数和尺度参数的三个集,然后使用位置参数和尺度参数 l0 和 s0 计算曲线的幅度或长度:
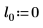 | 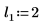 | 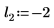 |
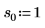 | 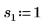 | 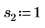 |
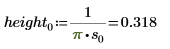
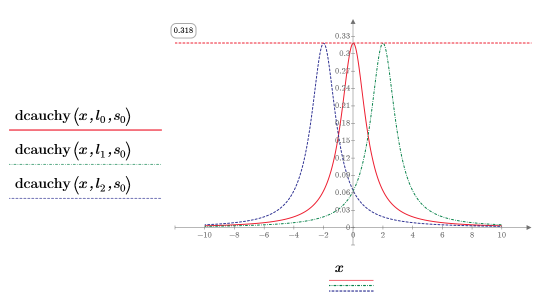
不同的位置参数值沿着 x 轴偏移曲线。
4. 使用一个固定的位置参数和不同的尺度参数值绘制 dcauchy 函数:
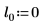 | 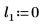 | 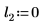 |
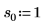 | 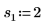 | 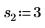 |
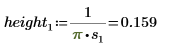
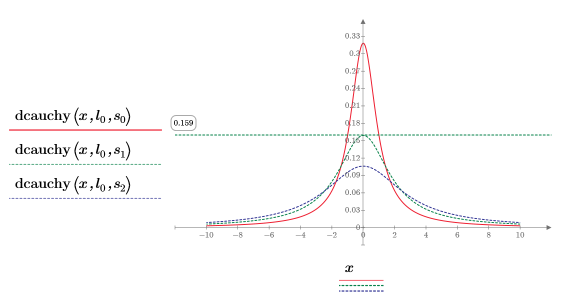
不同的尺度参数值可用于改变曲线高度。
5. 使用不同的位置参数值和尺度参数值绘制 dcauchy 函数:
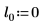 | 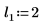 | 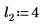 |
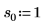 | 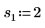 | 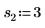 |
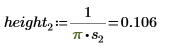
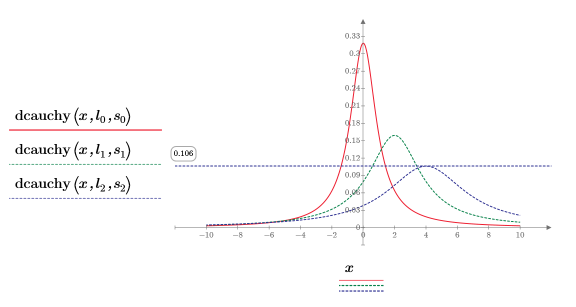
不同的尺度参数值和位置参数值可用于偏移曲线和改变曲线高度。
6. 使用不同的位置参数值和一个固定的尺度参数绘制 pcauchy 函数:
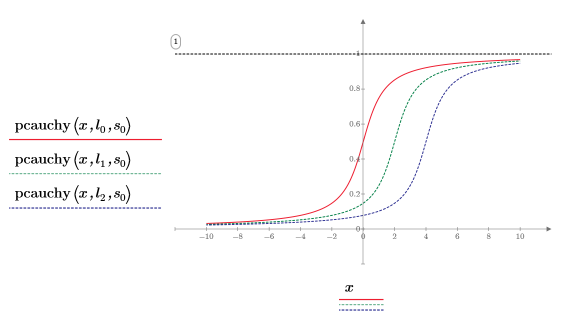
◦ 不同的位置参数值沿着 x 轴偏移曲线。
◦ 所有 pcauchy 的 y 值均介于 0 和 1 之间。
7. 使用一个固定的位置参数和不同的尺度参数值绘制 pcauchy 函数:
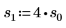
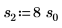
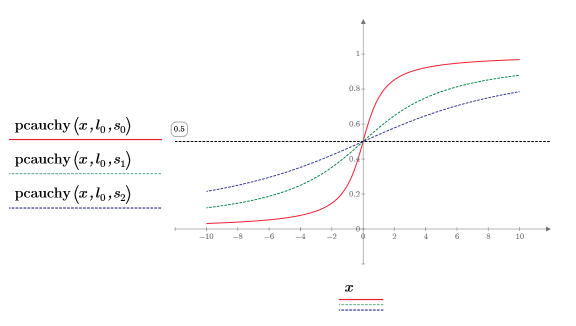
◦ 不同的尺度参数值将曲线水平展平,但是所有的曲线都在 y=0.5 处相交。
◦ 所有 pcauchy 的 y 值均落在 0 和 1 之间。
8. 使用不同的位置参数值和一个固定的尺度参数绘制 qcauchy 函数:
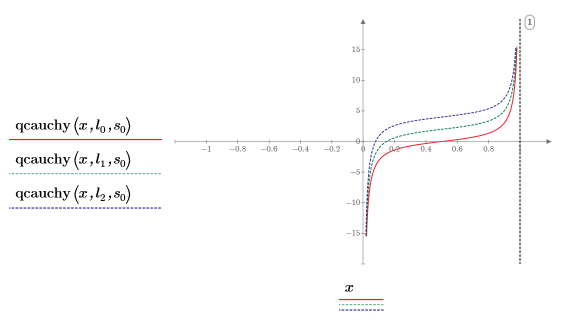
◦ 不同的位置参数值沿着 y 轴偏移曲线。
◦ 所有 qcauchy 的 x 值均落在 0 和 1 之间。
9. 使用固定的位置和尺度参数计算 rcauchy 函数:
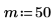
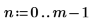
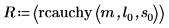
函数 rcauchy 返回由 m 个具有柯西分布的随机数字构成的矢量。
10. 绘制 rcauchy 函数所返回的随机数字。
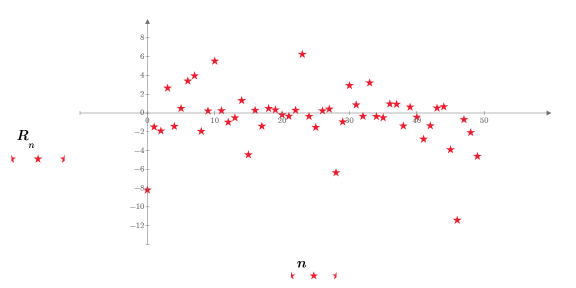
重新计算工作表会导致函数 rcauchy 返回一个新的随机数字集,相应地绘图也会进行更新。