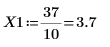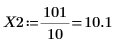示例:第二类贝塞耳函数
1. 定义两个步长值域变量:
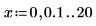
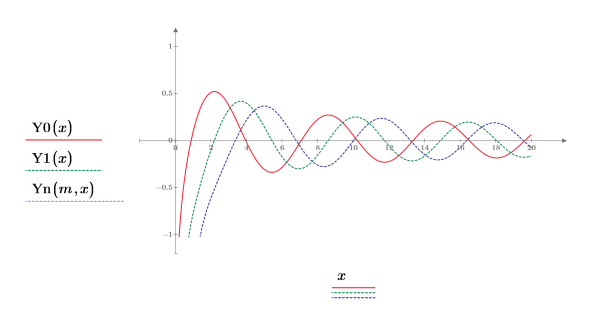
2. 绘制函数 Y0 和 Y1。在绘图中添加二阶函数 Yn:
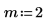
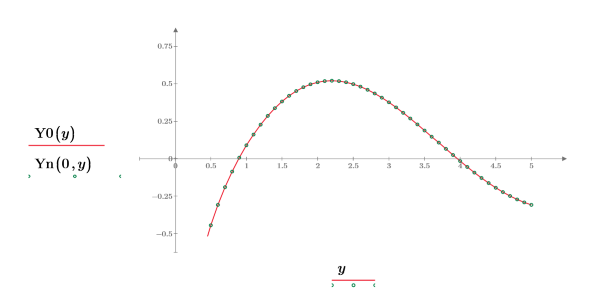
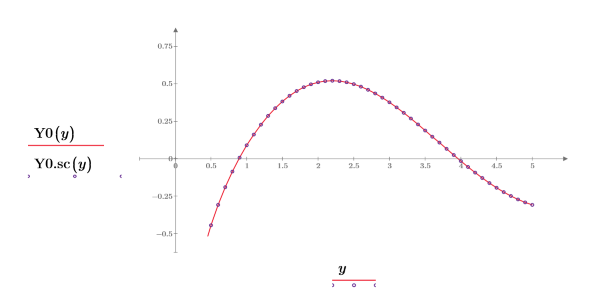
3. 创建绘图来显示 Y0(y)=Yn(0,y)。重新设置刻度值来放大 x 轴以便显示更多详细信息:
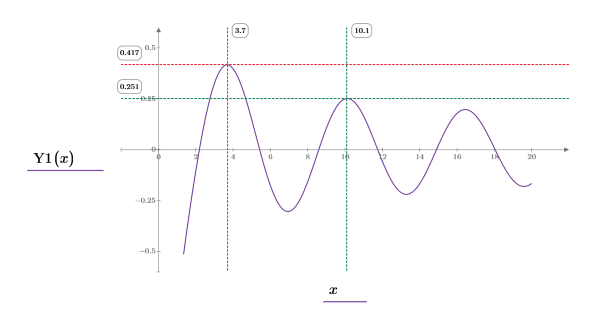
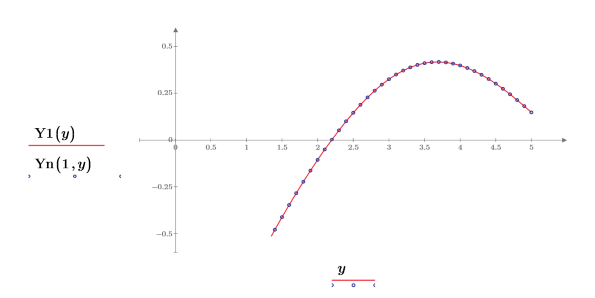
4. 创建绘图来显示 Y1(y)=Yn(1,y)。重新设置刻度值来放大 x 轴以便显示更多详细信息:
5. 使用符号运算来显示每个第二类贝塞耳函数和其缩放版本间的关系:
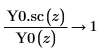
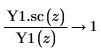
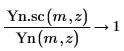
6. 创建绘图以显示:
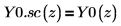
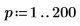
不在 0 处定义第二类贝塞耳函数。
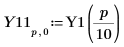
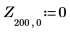
函数 localmax 需要一个具有两列的输入矩阵。函数 augment 可用于创建这样的矩阵。
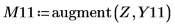
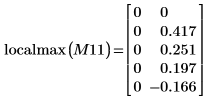
由于不在 0 处定义该函数,因此可以忽略在 (0, 0) 处的第一个局部极大值。
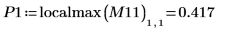
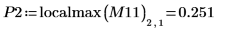
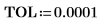
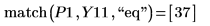
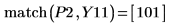
9. 在图像上添加标记来标记前两个峰值:
步长值域变量的步长为 0.1。这意味着在 1/10 出现峰值,在此分别由函数 match 或 3.7 和 10.1 来标识元素索引。