示例:贝塞耳函数
使用球形贝塞耳和球形汉克函数求出 3D 方形阱 (原子) 中薛定谔方程的解。
解表示所有的容许能量,能量为这些值时,内部和外部的波动函数拥有相同的值和一阶导数。对于角动量 (L) 的每个值,都存在这些能量。
1. 定义质量、普朗克常数和原子半径:
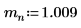
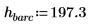
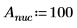
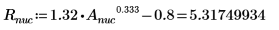
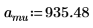
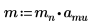
2. 将角动量设为零:
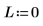
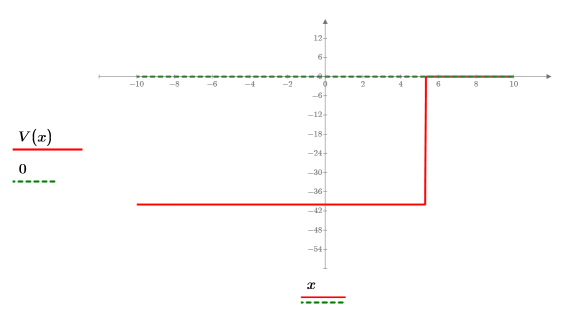
3. 定义并绘制势阱的势能:
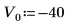
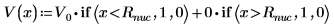
4. 使用球形贝塞耳函数和球形汉克函数来求解:
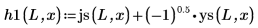
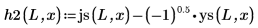
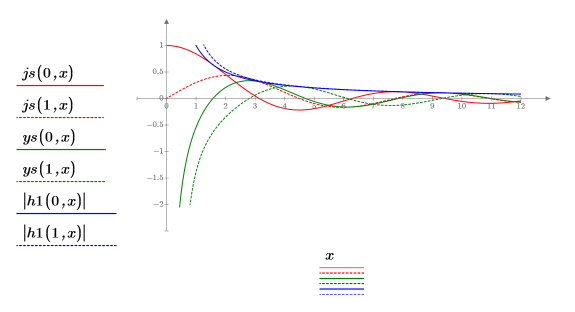
5. 定义边界状态 E < 0 的情况下势阱内部和外部第一能量状态解的波动函数:
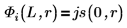
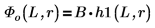
B 为相对正则化。
6. 定义传播常数:
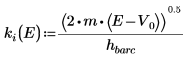
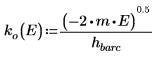
势阱外的解的自变量是假设的,因为势阱外面的波会衰减。
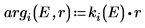
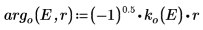
7. 匹配势阱边 (原子半径) 波函数以确定相对正则化:
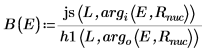
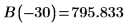
8. 匹配导数。通过查找导数相等位置来确定特征值。
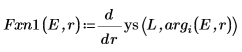
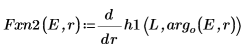
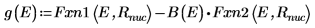
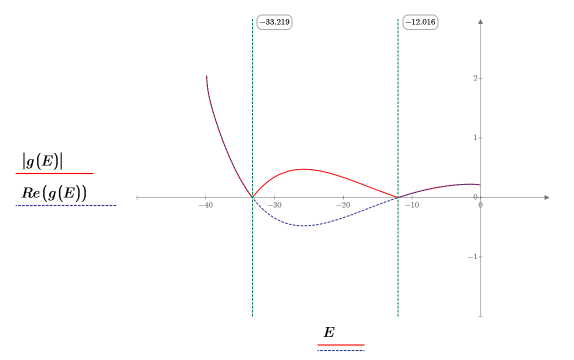
9. 提供 E 的两个估值:
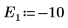
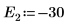
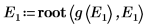
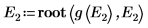
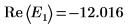
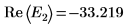
10. 绘制 g(E) 相对于 E 的图像,并添加竖直标记以显示两个根点: