示例:1 因子 ANOVA
1. 在测试一种新型合成纤维中棉纤维含量对其强度所具影响的实验中,定义因子数目。
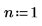
2. 定义实验中所用的 cotton (棉) 设置。
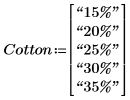
3. 使用函数 length 为因子定义阶数。
4. 调用函数 fullfact 创建代表实验及其游程的完全析因设计矩阵。
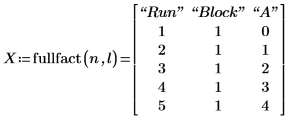
在设计矩阵 X 中,A 代表 cotton (棉) 因子,其水平以编码形式显示:
A 的编码值 | A 的实际值 |
|---|---|
0 | 15% |
1 | 20% |
2 | 25% |
3 | 30% |
4 | 35% |
5. 在第一个游程中测量棉纤维质量百分比为 15% 时合成纤维的强度。
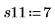
6. 对其他四个游程进行测量。
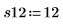
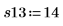
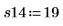
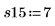
7. 调用函数 randomize 可打乱游程顺序。
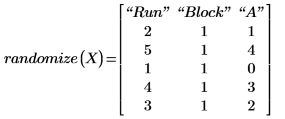
8. 以 randomize 函数所确定的顺序重复测量。
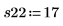
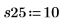
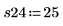
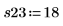
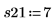
重复实验可有效地抵消非受控变量的影响。重复实验之前调用 randomize 函数有助于降低输入因子间任何程度的相关性。
9. 对所有需要重新进行的测量,重复步骤 7 和 8。将所有测量记录到矩阵 Y。

每列所包含的是每次重复的数据,每行所包含的是特定游程的数据。
10. 调用函数 boxplot 准备箱线图所需的数据,这种箱线图中每个箱对应一个游程。
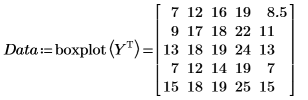
矩阵 Y 被转置,这是由于每个游程的结果均记录于矩阵的行,但用于 boxplot 的数据集必须是矩阵的列。
11. 调用函数 boxplotgraph。
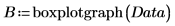
12. 创建箱线图。
a. 绘制 boxplotgraph 函数的输出:
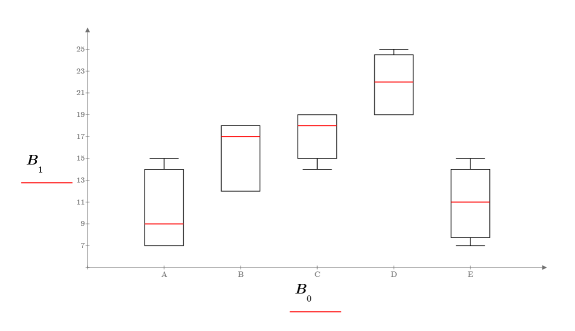
b. 使用标签为每个因子创建文本区域:
通过观察箱线图可发现,cotton (棉) 的质量百分比似乎对纤维的抗拉强度有所影响。纤维中 cotton (棉) 的质量百分比约为 30% 时,其抗拉强度达到最大。
13. 调用函数 anova 来测试棉的质量百分比是否影响抗拉强度。

14. 将 r 定义为运行数,将 x 定义为副本数,然后在 SSE 列计算平方和。
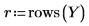
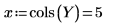
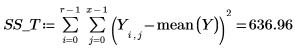
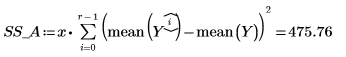
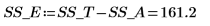
15. 将 N 定义为测量总数,然后在 df 列计算自由度。
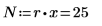
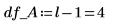
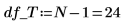
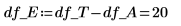
16. 在 MSE 列计算均方。
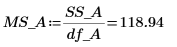
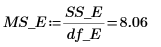
17. 为因子 A 计算 F-value。
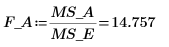
P 列中的 P-value 小于 0.05,表示因子 A 为显著因子。
18. 使用 F-value 验证 A 为显著因子的假设。计算 5% 显著性水平的临界 F 值。
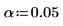
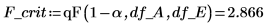
因子 A 的 F-value 大于临界 F 值,这再次证明了棉的质量百分比对纤维的抗拉强度有影响。
参考文献
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001. 62.