导数和求导运算符
|
运算符
|
说明
|
键盘快捷方式
|
|---|---|---|
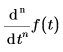 |
返回 f(t) 关于 t 的 n 阶导数,并计算其在 t 点处的值。
• 对于数值运算,n 是介于 0 和 5 之间的自然数 (包括 0 和 5)。
• 对于符号运算,n 可以是任意自然数。
|
Ctrl+Shift+D
|
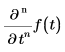 |
返回 f(t) 关于 t 的 n 阶偏导数,并计算其在 t 点处的值。
• 对于数值运算,n 是介于 0 和 5 之间的自然数 (包括 0 和 5)。
• 对于符号运算,n 可以是任意自然数。
|
Ctrl+D
|
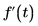 |
定义函数 g 为函数 f(t) 的一阶导数。
• 您可以级联 n 导数运算符,以获取 nth 阶导数。
• 对于数值或符号运算,可以有任意数量的导数运算符。但是,符号运算会快得多。
|
Ctrl+' (撇号)
|
操作数
• f(t) 为标量值函数。该函数可以是复数。
◦ 对于导数运算符,f(t) 可以是任意数量变量的函数。
◦ 对于导数运算符,f(t) 必须为唯一变量的函数。
• g 为函数名。
• t 是要进行求导运算的点。
附加信息
• 在计算表达式的一阶导数时,可将导数运算符的指数占位符留空。
• 一阶导数将被精确到 7 或 8 位有效数字内 (前提是进行求导运算的值与函数的奇异值不是非常接近)。导数的阶数每增加一阶,精度便会趋于减少约一个有效位数。
• 计算导数所使用的数值法是 Ridder 法的一种变化形式,它使用各种不同的步长大小来计算 (n + 1) 点均差,其中 n 为导数的阶。然后它将使用加权平均值来计算表中的连续近似值。会对连续的表格条目进行比较,然后将具有最小误差的表格条目作为导数返回 (如果误差在某个可接受的水平之下)。