특이값 분해
• svds(A) - 행렬 AH·A에 대한 eigenvalues의 양의 제곱근인 A의 특이값을 포함하는 벡터를 구합니다. 여기서, AH는 A의 공액 전치입니다. transpose 및 complex conjugate 연산자를 다음과 같이 사용하여 AH를 계산할 수 있습니다.
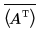
• svd(A) - 중첩 배열 3개의 벡터를 구합니다.
첫 번째 배열에는 svds에서 구한 특이값으로 이루어진 벡터 s가 포함되고, 다음 두 개의 배열은 A = U∙diag(s)·VH를 충족하는 행렬 U 및 VH입니다. 세 번째 항목 VH는 V의 공액 전치입니다.
세 번째 배열은 V가 아닌 VH입니다. 이것은 구한 배열에 공액 전치가 이미 적용되었다는 의미입니다. 따라서 다시 적용할 필요가 없습니다. 구한 배열을 수식에 직접 사용할 수 있습니다.
인수
• A는 m ≥ n인 m × n 배열입니다. svd의 경우 배열 요소가 실수여야 하지만, svds의 경우 복소수 값을 사용할 수 있습니다.
추가 정보
• 특이값은 항상 양의 실수입니다. 매우 작은 값은 0으로 해석되어야 합니다.
• svd 함수에는 Intel BLAS/LAPACK(Basic Linear Algebra Subprograms / Linear Algebra Package) 라이브러리가 사용됩니다.