다변수 다항식 회귀
• polyfit(X, Y, n/"terms"/M) - 행렬 Y에 기록된 결과를 행렬 X에 있는 데이터에 맞추는 다변수 다항식 회귀 표면을 설명하는 함수를 정의합니다. 문자열 “terms” 또는 행렬 M에 지정한 것처럼 항이나 다항식 차수 n으로 다항식 회귀 방정식을 정의할 수 있습니다. 다항 적합식에 절편을 포함하지 않으려는 경우에는 행렬 M을 사용합니다.
예를 들어 다음과 같은 다항식 회귀 함수 p를 생각해 볼 수 있습니다.
p := polyfit(X, Y ,1)
p(v) = 1.075
함수 p는 행렬 X에서 설명하는 대로 p의 독립 변수 각각에 대한 값을 지정하는 벡터 인수 v를 취합니다. 벡터 v의 각 변수는 행렬 X의 상응하는 열과 단위가 서로 호환되어야 합니다. 적합식 p를 통해 구하는 단위는 행렬 Y의 단위와 호환됩니다.
인수
• X는 각 열이 독립 변수를 나타내는 행렬 또는 설계 행렬입니다. X의 각 열은 단위가 서로 호환되어야 합니다.
• Y는 측정되거나 시뮬레이션된 결과로 이루어지는 벡터 또는 행렬이며, 각 행에는 X에 정의된 각 실행 또는 데이터 점에 대한 결과가 포함됩니다. 포함된 반복측정치의 수가 동일하지 않은 행이 있으면 Y의 빈 요소를 NaN으로 채워야 합니다. 행렬 Y의 요소는 단위가 서로 호환되어야 합니다.
• n은 다항식의 차수를 지정하는 정수입니다. 총 데이터 점 수 1 ≤ n ≤ length(Y) − 1보다 작아야 합니다. 그렇지 않으면 문제의 제약 조건이 부족하여 고유한 해를 구할 수 없게 됩니다.
• “terms”는 다항식 회귀에 포함할 항을 지정하는 문자열이거나, 인수 및 상호 작용을 지정하는 문자열입니다. "A B AB AA BB"는 다음 항을 포함하는 다항식을 의미합니다.
c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2
구분 기호로는 공백, 쉼표, 콜론 또는 세미콜론을 사용할 수 있습니다.
• M은 다항식을 지정하는 행렬입니다. 첫째 열에는 계수에 대한 추측값이 포함되고 나머지 열에는 각 항에 대한 독립 변수의 거듭곱이 포함됩니다. 앞서 설명한 다항식의 경우 M을 다음과 같이 정의합니다.
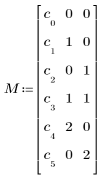
추가 정보
regress 함수의 출력은 적합식을 구하기 위해 interp 함수로 전달되는 계수의 행렬입니다.
polyfit 함수의 출력은 적합식 자체이기 때문에 interp 함수를 호출할 필요가 없습니다.