감마 함수
• Γ(z) - z의 오일러(Euler) 감마 함수 값을 구합니다.
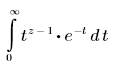
감마 함수와 관련하여 다음 관계가 유용할 수 있습니다.
◦ Γ(z + 1) = z · Γ(z)
◦ Γ(z)·Γ(1 − z) = π · csc(π · z)
◦ Γ(n + 1) = n!
• Γ(a, x) - 매개변수가 a인 x의 불완전 감마 함수 값을 구합니다. Γ(a, 0) = Γ(a).
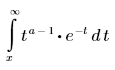
• lnΓ(z) - z에서 계산된 오일러 감마 함수의 자연 로그를 구합니다.
Γ를 입력하려면 G를 누르고 Ctrl+G를 누릅니다.
lnΓ 함수를 사용하여 더 작은 결과를 반환한 다음 배율을 조정할 수 있습니다.
• Psi(y) - Γ(y) 함수의 자연 로그 도함수를 구합니다.
인수
• z는 z = 0, −1, −2...에 대해 정의되지 않은 단위 없는 실수 또는 복소수 스칼라 값입니다.
Γ(z)의 경우 −107 ≤ Re(z) ≤ 171 및 −106 ≤ Im(z) ≤ 106 인수만 수치 오버플로 없이 계산할 수 있습니다. 복소수 z의 경우 Γ(z)는 실함수의 분석 접속입니다.
• a는 단위 없는 양의 실수 스칼라 값입니다.
• x는 단위 없는 양의 실수 스칼라 값 또는 0입니다.
• y는 실수입니다.