常微分方程式の求解
ソルブブロックおよびodesolve関数を使用して、一定の範囲内の値について常微分方程式 (ODE) を満たす関数を求めることができます。
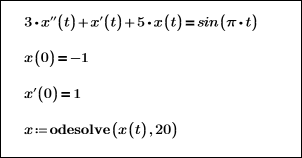
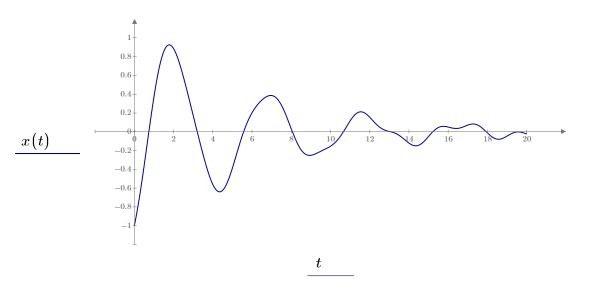
ここでは、 0 ≤ x ≤ 20 の範囲で出力関数の解を求めます。
ソルブブロックで ODE を使用する場合、以下の制約条件が適用されます。
• 演算子 - 「等しい」演算子を使用して常微分方程式を解きます。比較演算子や「等しくない」演算子は使用しないでください。導関数を定義する場合、d/dx や d2/dx2 などの微分演算子、あるいは y'(x) や y''(x) などのプライム演算子を使用します。
• 初期条件と境界条件 - 単一の n 階常微分方程式では、n 個の独立等式制約条件が必要です。
◦ 初期値問題 - y(x) および n − 1 次までの各導関数の単一の始点 a における値が必要です。
◦ 境界値問題 - n 個の制約条件によって、始点 a または終点 b における y(x) およびその導関数の特定の値を指定する必要があります。これらの制約条件は、sbval関数への入力の要件を満たす必要があります。境界値条件を指定した場合に odesolve は sbval を呼び出します。
いずれの場合も、境界条件で使う終点は、odesolve コマンドで指定した終点と同じでなければなりません。PTC Mathcad で条件の種類と数がチェックされ、正しくない場合はエラーが返されます。
初期条件の設定では微分 dy/dx のライプニッツの記法はサポートされていません。代わりに、ラグランジュの記法と呼ばれるプライム演算子 y’ を使用してください。 |
• 代数制約条件 - y(b) + z(b) = w(b) などの代数制約条件を追加できます。odesolve の出力関数の 1 つとして指定する必要がある未知関数 w がソルブブロックに追加されます。
• 出力 - odesolve の出力値を、引数を使わずに、1 つの関数名、または複数の関数名のベクトルに割り当てる必要があります。
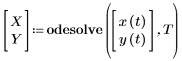
これらの関数の暗黙的な引数は積分変数です。
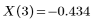
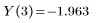
解法
• 問題の大きさと相対ステップサイズに基づいて、TOL の値を減らして、適切な解を求める必要があります。PTC Mathcad odesolve から積分のステップ数が多すぎることが報告された場合に、この方法を試してください。
• 解く関数の積分区間に特異点が含まれていてはなりません。特異点が含まれている場合、信頼性が低い結果が返る可能性があります。
• 同じ動作が周期的に何回も繰り返される問題を解く場合、エイリアシングが起きることがあります。予想どおりの周波数を結果として得るには、補間点を増やします。
• 最高次の導関数項が線形でない常微分方程式を解くか、プログラムループ内で常微分方程式を解くには、rkfixedまたはその他のコマンドライン ODE ソルバーのいずれかを使用します。ローカル関数を使用して、パラメータ化されたソルブブロックの出力をプログラムループ内で割り当てることもできます。