特異値分解
• svds(A) - A の特異値である行列 AH.Aeigenvalues の正の平方根(AH は A の共役転置) を含むベクトルを返します。次のように、演算子 transpose および complex conjugate を使用して AH を計算できます。
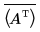
• svd(A) - 3 つの入れ子配列のベクトルを返します。
最初の配列には、svds によって返る特異値のベクトル s が含まれています。次の 2 つの配列は、A = U∙diag(s)·VH を満たす行列 U と VH です。3 つ目のエントリ VH は V の共役転置です。
3 つ目の配列は V ではなく VH です。これは、返った配列に共役転置が適用済みであることを意味します。再度適用する必要はありません。返った配列は、式で直接使用できます。
引数
• A は m × n の配列で、m ≥ n です。svd の配列要素は実数でなければなりません。これに対して、svds の配列要素には複素数値を使用できます。
追加情報
• 特異値は常に正の実数です。ごく小さな値は 0 と解釈されます。
• svd 関数は Intel Basic Linear Algebra Subprograms (BLAS)/Linear Algebra Package (LAPACK) ライブラリを使用します。