ガンマ関数
• Γ(z) - z のオイラーのガンマ関数の値を返します。
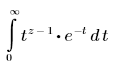
ガンマ関数を使った、次のような便利な公式があります。
◦ Γ(z + 1) = z · Γ(z)
◦ Γ(z)·Γ(1 − z) = π · csc(π · z)
◦ Γ(n + 1) = n!
• Γ(a, x) - パラメータ a を持つ x の不完全ガンマ関数の値を返します。Γ(a, 0) = Γ(a).
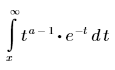
• lnΓ(z) - z におけるオイラーのガンマ関数の自然対数を返します。
Γ を入力するには、G を押してから Ctrl + G キーを押します。
lnΓ 関数を使用して小さな結果を求めてから、尺度を変更することもできます。
• Psi(y) - Γ(y) 関数の自然対数の導関数を返します。
引数
• z は、無次元の実数または複素数のスカラーです。z = 0, −1, −2... の場合は未定義です。
Γ(z) の場合、数値のオーバーフローなしで評価できる引数は −107 ≤ Re(z) ≤ 171 と −106 ≤ Im(z) ≤ 106 だけです。z が複素数のときは、Γ(z) は実数関数の解析的継続になります。
• a は無次元の正の実数のスカラーです。
• x は無次元の正の実数のスカラーまたは 0 です。
• y は実数です。