例: 極限演算子の使用
極限値として無限大の使用
1. 極限演算子を使用して、引数が無限大に近づく式をシンボリック評価します。
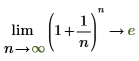
2. 表示が見やすいように関数をプロットします。横マーカーを使用して e を示します。
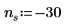 | 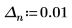 | 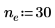 |
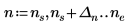 | ||
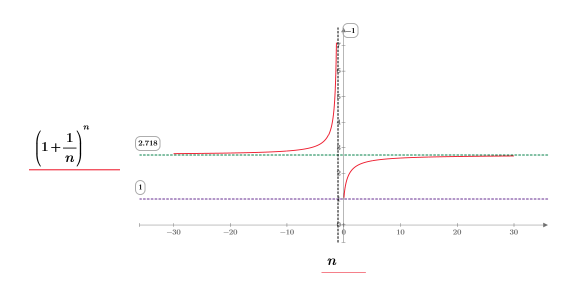 | ||
(x, y) 象限で次の事項が確認されます。
◦ n が positive infinity に近づくと、関数は y=e に近づきます。
◦ n が 0 に近づくと、関数は y=1 に近づきます。
数学上、これは次のシンボリック評価で表されます。
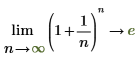 | 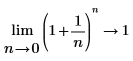 |
(-x, y) 象限で次の事項が確認されます。
◦ n が negative infinity に近づくと、関数は y=e に近づきます。
◦ n が -1 に近づくと、関数は y=infinity に近づきます。
数学上、これは次のシンボリック評価で表されます。
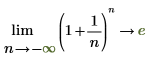 | 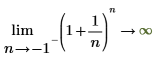 |
2 つ目の式で使用されている左極限方向は、曲線の左側から -1 に近づくことを意味します。これが指定されていない場合、-1 < n < 0 に対して関数が定義されていないため、"undefined" が返されます。 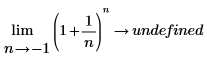 |
極限の方向の使用
1. cot 関数をプロットします。
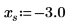 | 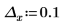 | 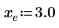 |
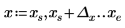 | ||
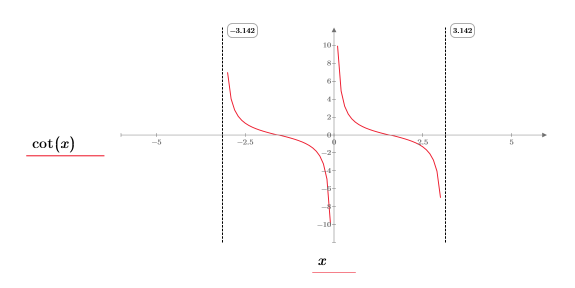 | ||
(x, y) 象限で次の事項が確認されます。
◦ x が 0 に近づくと、関数は y=infinity に近づきます。
◦ x が π に近づくと、関数は y=-infinity に近づきます。
数学上、これは次のシンボリック評価で表されます。
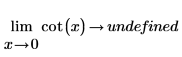 | 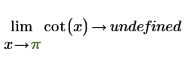 |
この関数は x=+/- n*π/2 付近で対称なので、シンボリック評価は "undefined" を返します。これは、この関数が x=0 (および π の倍数) 付近で、x が 0 に近づく方向によって infinity または -infinity になるためです。
これは "極限の方向" の指定が適切な事例です。
2. "極限の方向" を指定してから、0 および π 付近で cot 関数を再評価します。
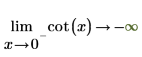 | 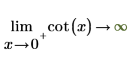 |
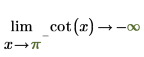 | 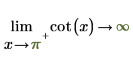 |
返される結果は、プロットと一致します。
関数をプロットすると、視覚化して、シンボリック評価の結果を再確認するために役立つ場合があります。 |