例: 信号および信号のタイプ
信号は、物理量または物理変数を表す関数でありデータセットです。通常、信号は、物理現象 (抵抗器を流れる電流、水中を伝搬するソナー音波、地震など) の振る舞いについての情報を含んでいます。数学的には、信号は、独立変数 t (一般的には時間を表す) の関数として表されます。つまり、信号は x(t) として表されます。
連続時間信号と離散時間信号
信号 x(t) は t が連続変数の場合には連続時間信号になります。t が離散変数の場合、つまり x(t) が離散時間で定義されている場合、x(t) は離散時間信号となり、x(n) として表されます (ここで、n は整数)。離散時間信号 x(n) は、株価の終値など、独立変数が本質的に離散的である現象を表すものと、連続時間信号 x(t) を t = nT でサンプリングすることによって得られるものがあります (ここで、T はサンプリング期間)。
以降の例は主に離散時間信号での例です。典型的な離散時間信号のいくつかの例を次に示します。
単位ステップ信号
1. ヘビサイドのステップ関数を使用して単位ステップ関数を定義します。
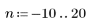
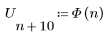
このヘビサイドステップ関数は f(0)=0.5 です。
2. 範囲を定義して単位ステップ関数をプロットします。
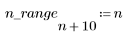
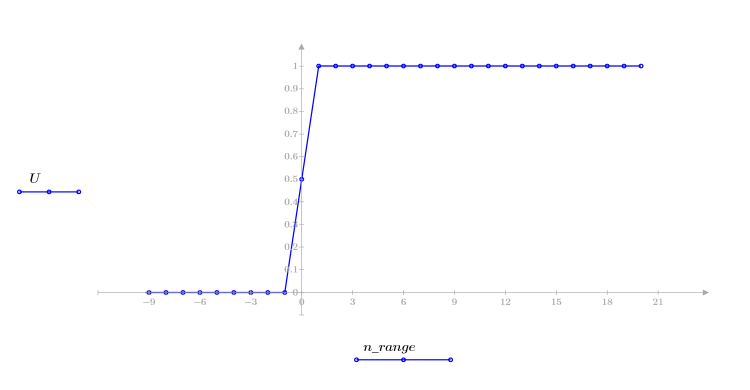
単位インパルス信号
1. 単位インパルス関数を定義します。
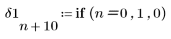
2. 単位インパルス関数をプロットします。

3. k の値を設定して、インパルスを k サンプルだけ右にシフトします。
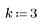
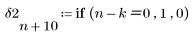
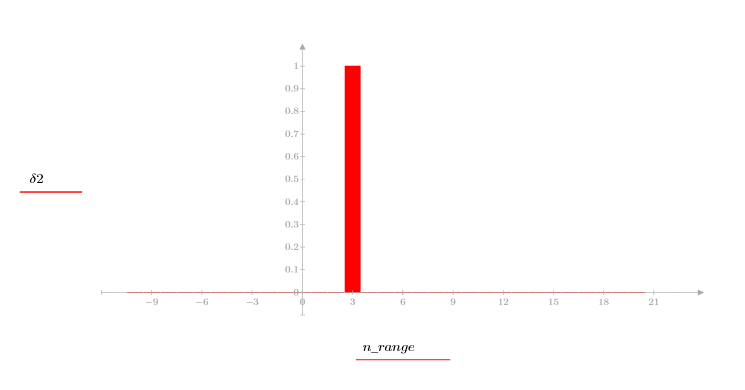
正弦信号
1. 周波数を設定します。
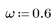
2. 正弦関数を定義します。
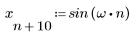
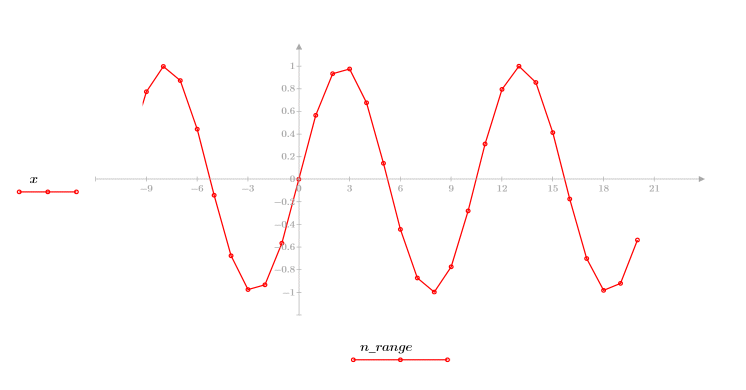
3. sinusoidal 関数をプロットします。
指数信号
1. 係数αを設定します。
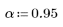
2. 指数関数を定義します。
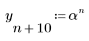
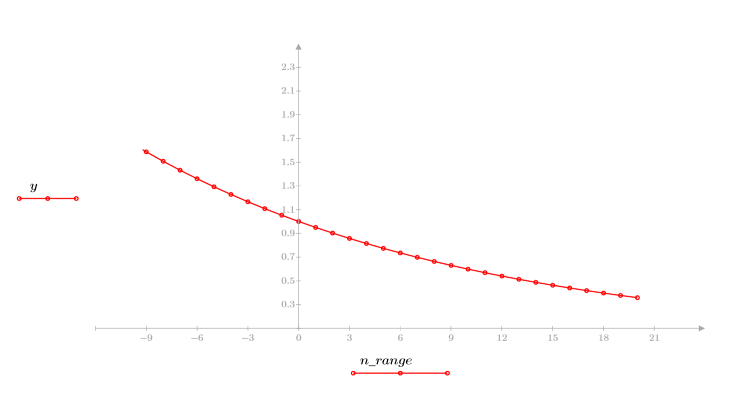
3. 指数関数をプロットします。
指数減衰正弦波
正弦関数と指数関数の積から成る関数をプロットします。
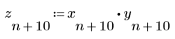
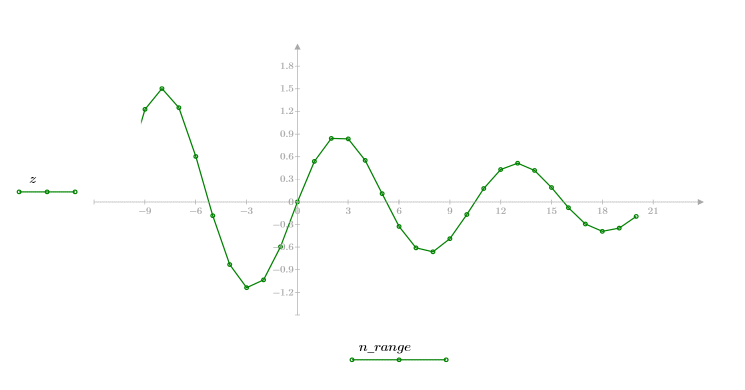
指数減衰正弦関数が返ります。
アナログ信号とデジタル信号
連続時間信号 x(t) が連続時間区間内で任意の値をとりうる場合、x(t) をアナログ信号と呼びます。離散時間信号 x(n) がとりうる値の数が有限である場合、x(n) をデジタル信号と呼びます。アナログ信号をデジタル信号に変換するには、アナログ信号をサンプリングして量子化する必要があります。
実数信号と複素信号
信号 x(t) は、その値が実数の場合には実数信号になります。同様に、信号 x(t) は、その値が複素数の場合には複素信号になります。関数phaseおよびphasecorを使用して、複素信号を操作します。
確定信号とランダム信号