例: 2 次応答面

関数 > 実験計画 > 回帰分析 > 例: 2 次応答面

例: 2 次応答面

関数boxwilson、polyfitc、およびpolyfitを使用して、実験を計画し、調査中のプロセスのモデルを作成します。ソルブブロックを使用して、モデルによって予測される最大収率を求めます。

1. boxwilson 計画行列を定義します。

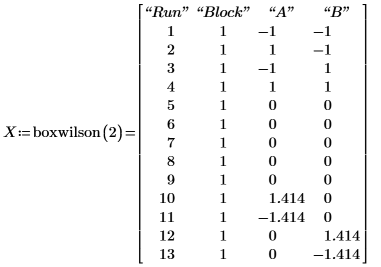
2. 調査中の化学工程の自然変数である A (反応時間: 分) と B (華氏温度) に実際の値を定義します。

3. doelabel関数を呼び出して、計画行列の符号化された値を自然変数の実際の値に変換します。

<region id="ID0EODKW" top="729.60000000000014" left="19.200000000000003" height="267.4" width="397.84666666666669" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="55">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">D</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">doelabel</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Vals</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="14,8" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

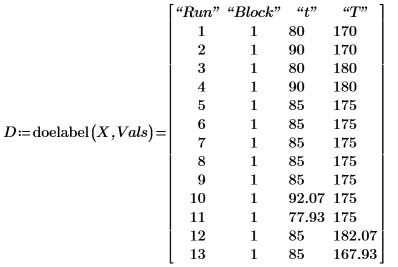
4. ランごとの化学工程の収率を記録します。

5. polyfitc を呼び出して、符号化された値を使用して 2 次多項式回帰を実行します。

6. polyfitc の出力から回帰係数を抽出します。

<region id="ID0EEIKW" top="1420.8000000000002" left="19.200000000000003" height="34" width="158.86333333333334" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="61">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">c</id>
      <apply>
        <matcol />
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyfitc</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
            <real>2</real>
          </sequence>
        </apply>
        <real>1</real>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="14,8" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

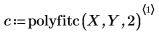
7. 化学反応をモデル化する、符号化された値を使用した関数を作成します。この関数を使用して、A=-1 かつ B=1 における収率を予測します。

<region id="ID0E3JKW" top="1516.8000000000002" left="19.200000000000003" height="38.952000000000005" width="381.2766666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="63">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="VARIABLE" xml:space="preserve">yield</id>
        <boundVars>
          <id labels="VARIABLE" xml:space="preserve">A</id>
          <id labels="VARIABLE" xml:space="preserve">B</id>
        </boundVars>
      </function>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <plus />
            <apply>
              <plus />
              <apply>
                <plus />
                <apply>
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c</id>
                  <real>1</real>
                </apply>
                <apply>
                  <mult />
                  <apply>
                    <indexer />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c</id>
                    <real>2</real>
                  </apply>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
                </apply>
              </apply>
              <apply>
                <mult />
                <apply>
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c</id>
                  <real>3</real>
                </apply>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
              </apply>
            </apply>
            <apply>
              <mult />
              <apply>
                <mult />
                <apply>
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c</id>
                  <real>4</real>
                </apply>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
              </apply>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
            </apply>
          </apply>
          <apply>
            <mult />
            <apply>
              <indexer />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c</id>
              <real>5</real>
            </apply>
            <apply>
              <pow />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">A</id>
              <real>2</real>
            </apply>
          </apply>
        </apply>
        <apply>
          <mult />
          <apply>
            <indexer />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c</id>
            <real>6</real>
          </apply>
          <apply>
            <pow />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">B</id>
            <real>2</real>
          </apply>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="14,8" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

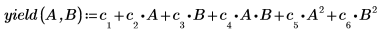
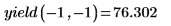
8. polyfit を呼び出して、化学反応をモデル化する、実際の値を使用した関数を作成します。この関数を使用して、t=80 分かつ T=170F における収率を予測します。

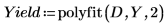
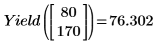
予想どおり、計算された収率は手順 7 で予測された値と同じです。

9. ソルブブロックを使用して最大収率を求めます。

<region id="ID0EHOKW" top="1824.0000000000002" left="38.400000000000006" height="196" width="300" xmlns="http://schemas.mathsoft.com/worksheet50">
  <solveblock>
    <regions>
      <region id="" top="24" left="24" solve-block-category="guess-value">
        <math resultRef="71">
          <define xmlns="http://schemas.mathsoft.com/math50">
            <id labels="VARIABLE" xml:space="preserve">a</id>
            <real>85</real>
          </define>
          <resultFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
            <matrix size="14,8" offset="0,0" show-indices="false" expand-nested-arrays="false" />
          </resultFormat>
        </math>
      </region>
      <region id="" top="48" left="24" solve-block-category="guess-value">
        <math resultRef="73">
          <define xmlns="http://schemas.mathsoft.com/math50">
            <id labels="VARIABLE" xml:space="preserve">b</id>
            <real>175</real>
          </define>
          <resultFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
            <matrix size="14,8" offset="0,0" show-indices="false" expand-nested-arrays="false" />
          </resultFormat>
        </math>
      </region>
      <region id="" top="96" left="19.2" solve-block-category="guess-value">
        <math resultRef="75">
          <define xmlns="http://schemas.mathsoft.com/math50">
            <function>
              <id labels="VARIABLE" xml:space="preserve">f</id>
              <boundVars>
                <id labels="VARIABLE" xml:space="preserve">a</id>
                <id labels="VARIABLE" xml:space="preserve">b</id>
              </boundVars>
            </function>
            <apply>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Yield</id>
              <matrix rows="2" cols="1">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">a</id>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
              </matrix>
            </apply>
          </define>
          <resultFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
            <matrix size="14,8" offset="0,0" show-indices="false" expand-nested-arrays="false" />
          </resultFormat>
        </math>
      </region>
      <region id="" top="153.6" left="19.2" solve-block-category="solver">
        <math resultRef="77">
          <define xmlns="http://schemas.mathsoft.com/math50">
            <matrix rows="2" cols="1">
              <id labels="VARIABLE" xml:space="preserve">t_max</id>
              <id labels="VARIABLE" xml:space="preserve">T_max</id>
            </matrix>
            <apply>
              <id labels="KEYWORD" xml:space="preserve">maximize</id>
              <sequence>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
                <id xml:space="preserve">a</id>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
              </sequence>
            </apply>
          </define>
          <resultFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
            <matrix size="14,8" offset="0,0" show-indices="false" expand-nested-arrays="false" />
          </resultFormat>
        </math>
      </region>
    </regions>
  </solveblock>
</region>

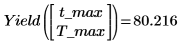
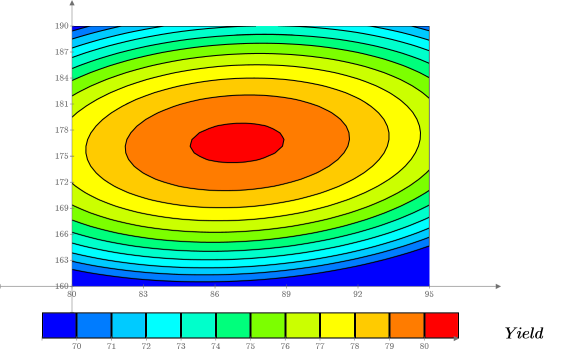
10. 等高線図を使用して t_max と T_max における収率の変化を視覚化します。

<region id="ID0EXRKW" top="2611.2000000000003" left="38.400000000000006" height="353.54124986559123" width="573.493675381802" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="transparent">
    <contourPlot>
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="80" end="95">
          <axisLine position="ticknumberlock" positionticmark="0" legendWidth="0" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="87">
              <real xmlns="http://schemas.mathsoft.com/math50">80</real>
            </startValue>
            <secondTickValue resultRef="89">
              <real xmlns="http://schemas.mathsoft.com/math50">83</real>
            </secondTickValue>
            <endValue resultRef="91">
              <real xmlns="http://schemas.mathsoft.com/math50">95</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="160" end="190">
          <axisLine position="ticknumberlock" positionticmark="0" legendWidth="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="93">
              <real xmlns="http://schemas.mathsoft.com/math50">160</real>
            </startValue>
            <endValue resultRef="95">
              <real xmlns="http://schemas.mathsoft.com/math50">190</real>
            </endValue>
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="70" end="80">
          <axisLine position="origin" positionticmark="5" legendWidth="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <zDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="97">
              <real xmlns="http://schemas.mathsoft.com/math50">70</real>
            </startValue>
            <endValue resultRef="99">
              <real xmlns="http://schemas.mathsoft.com/math50">80</real>
            </endValue>
          </zDomain>
        </zAxis>
      </axes>
      <contour color="#FF000000" show-lables="false" resultRef="100" />
      <graph-size width="475.603675381802" height="292.00730756823805" />
      <plotEquation>
        <math resultRef="101">
          <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Yield</id>
        </math>
        <math resultRef="102">
          <placeholder xmlns="http://schemas.mathsoft.com/math50" />
        </math>
      </plotEquation>
    </contourPlot>
  </plot>
</region>

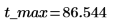
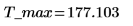
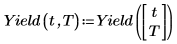
参考文献

Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, pp. 442.