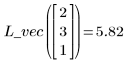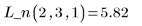例: 区分 2 次適合
単変量多項式回帰
loess関数を使用して、局所回帰によって一連の 2 次関数をデータに適合させます。
1. 次の行列を定義します。

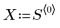
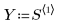
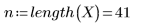
2. スパンを定義 - loess 関数による一連の 2 次適合に使用されるスパン、つまり各データ点を囲む重み付けウィンドウ内の点の総数の割合。
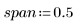
1 より大きい点の数を平均して各最小二乗加重適合で使用するので、一般的なガイドラインとしては (span*n) は 1 より大きくなければなりません。
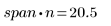
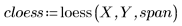
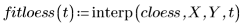
4. polyfit関数を呼び出して、2 次多項式をデータセットに適合させます。
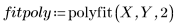
5. 上記で定義した 2 本の曲線をプロットします。
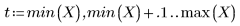
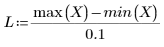
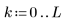
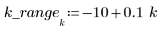
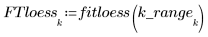
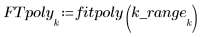
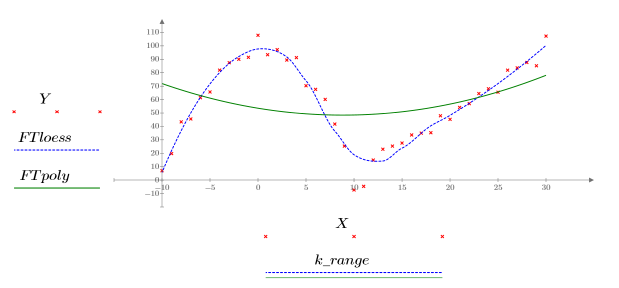
• スパンが大きい (2 や 3 など) 場合、そのデータは重みがほぼ等しい単一の 2 次適合であると見なされます。この適合は polyfit の 2 次多項式の解に近づきます。
• スパンを選択するときの具体的なガイドラインはありません。スパンが大きくなるに従い、適合で接続される区分の数が減るので、loess 適合のプロットは滑らかになります。ただし、そのような適合にはデータの特性が適切に反映されないことがあります。逆に、スパンが小さくなると、loess が収束しないことがあります。
• loess のアルゴリズムは外挿を目的としたものではありません。元の x の範囲にない値で interp を計算しようとすると、エラーが返ります。
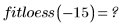
• データに不連続性があるときに、区分適合を手動で実行したくない場合や、複雑な、物理的に非現実的な非線形適合方法を使用したくない場合、loess を使用できます。
多変量多項式回帰
loess 関数を使用して多変量多項式回帰を実行します。loess 関数では 5 つ以上の独立変数は適合できません。
1. データセットを定義します。
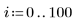
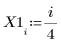
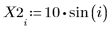
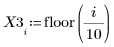
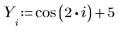
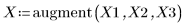
2. 平滑化パラメータを定義します。
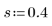
このパラメータの意味は単変量の場合と同じです。
3. loess 関数を呼び出します。
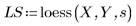
4. interp 関数を呼び出して多変量適合関数を補間します。この適合関数は、n 成分ベクトルまたは n 個の引数をとります (ここで、n は独立変数の数)。
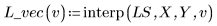
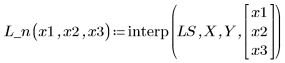
5. 適合関数を使用して、点 (2, 3, 1) における Y の値を予測します。