例: 非線形回帰 2
LeastSquaresFit関数を使用して非線形回帰を実行します。LeastSquaresFit ソルバは、非線形回帰問題を解く場合に最も柔軟性が高い方法です。このソルバでは、任意の依存パラメータの制約方程式、パラメータの下限と上限、x の値の標準偏差、計算の信頼限界を指定できます。
LeastSquaresFit
1. データセットを定義します。
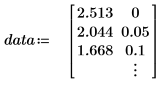
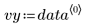
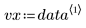
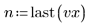
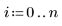
このデータは NIST の Web サイトに掲載されている例から抜粋されています。このデータは次の方程式を使用して 14 桁の精度で生成されています。
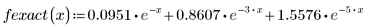
2. 適合関数を定義します。
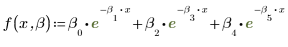
上記の個々のパラメータは、ベクトル β の成分です。ベクトルの成分でなく、独立変数名を使用して入力関数を指定することもできます。
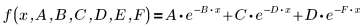
3. 推定値を指定します。
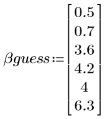
4. パラメータの信頼限界を定義します。
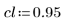
5. LeastSquaresFit 関数を呼び出します。
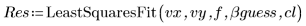
このソルバでは、逐次 2 次計画法 (SQP) を使用して最小二乗問題の解が求められます。追加の変数を導入することで、元の問題が汎用等式制約付き非線形計画問題に変換されます。これは一般的にはその他の手法よりも高速で安定性の高い手法です。
6. LeastSquaresFit 関数によって返された出力ベクトルを表示します。
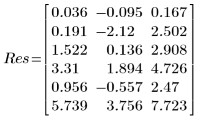
◦ 出力の 1 列目には適合パラメータの値が格納されています。2 列目にはパラメータの信頼区間の左側境界が格納され、3 列目には右側境界が格納されています。
◦ 信頼水準 95% でのパラメータの信頼区間の幅がかなり広くなっているので、この適合は困難であり、個々のパラメータが大きく変化する可能性があることがわかります。この結果、適合パラメータの値は NIST の Web サイトに掲載されている正確な値とは異なっています。
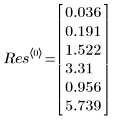

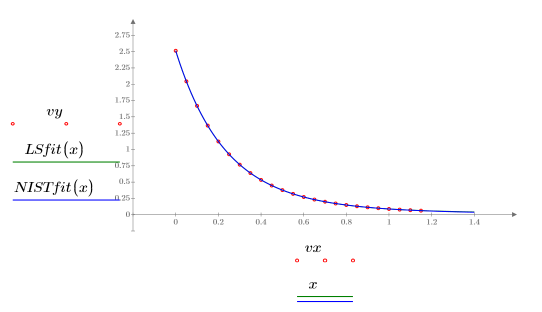
7. データ、最小二乗適合、NIST のデータを利用した適合をプロットします。
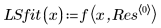
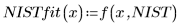
8. 最小二乗適合を元のデータと比較します。
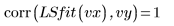
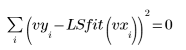
適合は収束に近づいていますが、収束許容誤差を調整することで良好な結果が得られる場合があります。このためには、LeastSquaresFit 関数のいずれかのオプションの引数を指定します。
制約条件、標準偏差、許容誤差
LeastSquaresFit では、オプションの引数を指定できます。
• 標準偏差ベクトル
• 下限と上限の行列
• 精度
オプションのいずれかの引数を単独で使用することも可能ですが、複数の引数を入力する場合、指定する順序が重要です。
1. 1 つのデータ値を摂動して誤測定をシミュレートします。
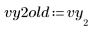
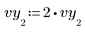
2. 適合の値の下限と上限を指定します。
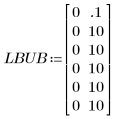
この場合には下限と上限がわからないので、下限と上限はとりうるパラメータ値の十分外側に設定しています。
3. y の各値の標準偏差のベクトルを設定して外れ値をマスクします。
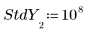
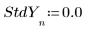
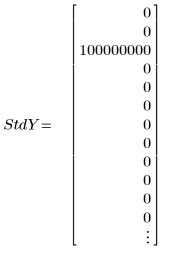
◦ 108 という大きな値の標準偏差によって、誤った測定値が計算から実質的に除去されています。
◦ LeastSquaresFit 関数の引数として標準偏差のベクトルを指定した場合、ソルバによって次の関数が最小化されます。
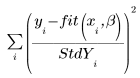
ある点における標準偏差が 0 の場合、その点では元の偏差がない関数が使用され、StdYi が 1 に設定されます。
4. 計算により厳格な収束許容誤差が適用されるように精度を設定します (デフォルトは 10-7)。
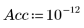
5. 標準偏差を指定する方法と指定しない方法で LeastSquaresFit 関数を呼び出します。
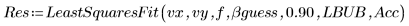
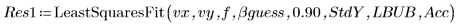
◦ 信頼限界が大きすぎるので、マスクしていない計算は失敗します。
◦ 新しいパラメータは NIST の値に近くなります。
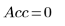
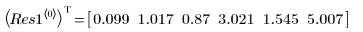
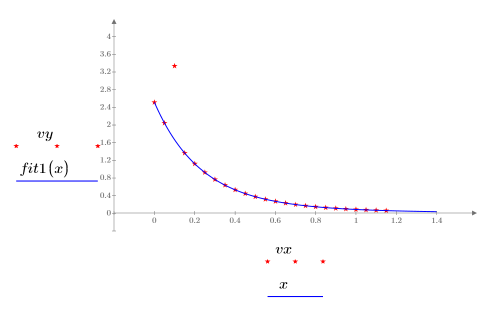
6. 外れ値とマスクした適合を含むデータをプロットします。
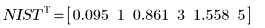
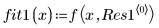
参考文献
この例で用いたデータは、NIST の Statistical Reference Datasets アーカイブに記載されている Lanczos, C., Applied Analysis, Prentice Hall, 1956 (ページ 272 から 280) から抜粋したものです。