例: ノイズジェネレータ
白色ノイズ
whiten関数は、ランダム出力が -0.5 から 0.5 の範囲の一様分布に従う N 個のソースによって生成されるノイズをシミュレートします。
1. whiten 関数を使用して、6 個のノイズソースで白色ノイズ関数を評価します。

whiten 関数は、計算するたびに異なるベクトル成分を返します。
2. 比較的大きな出力ベクトルについて考えます。
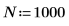
3. 白色ノイズ関数をプロットします。
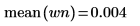
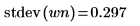
5. 理論上の平均値を示してから、var 関数を使用して標準偏差を計算します。
プロットによって、wn 信号の理論上の平均値が 0 であることが示されます。 | |
標準偏差は分散の平方根として求められます。 | 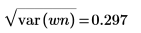 |
6. 計算された平均値と標準偏差の値をその理論値と比較し、両者に大きな違いがないことを確認します。
ガウスノイズ
gaussn 関数は、平均値 0、標準偏差 1 のガウス確率分布に従う x 個のノイズソースをシミュレートします。
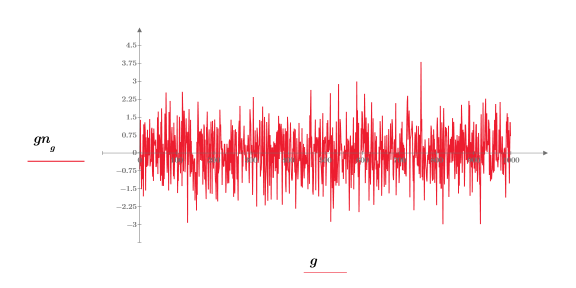
1. 6 個のノイズソースで gaussian ノイズ関数を評価します。

ベクトルの成分は理論上あらゆる実数を含むことができますが、ほとんどの場合は -3 から +3 の範囲内になります。これを確認するには F5 キーを押して関数を再計算します。
2. サンプルのガウスシーケンスをプロットします。
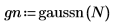
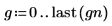
3. 値を幅 0.5 の 20 個の区間に分けることで、ベル形のヒストグラムをプロットするためのガウスデータを準備します。
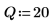
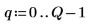
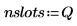
4. 区間の境界が格納されるベクトルを定義し、右端の境界を設定します。
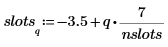
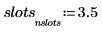
5. hist 関数を使用してヒストグラムを作成し、棒グラフとしてプロットします。
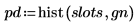
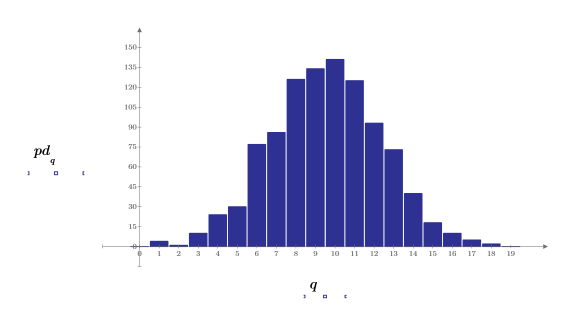
6. サンプルの平均値と標準偏差を期待値 0 および 1 と比較します。
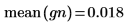
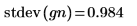
1/f ノイズ
onefn 関数は、Richard Voss によって考案されたアルゴリズム (Scientific American, April 1978 の Martin Gardner のコラムを参照) に基づいたルーチンを使用して、1/f ノイズの近似値を計算します。
1. onefn 関数を使用して、1000 個の点を持つ 1/f ベクトルを生成します。
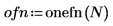
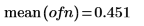
2. 平均値が 0 になるように調整します。
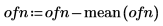
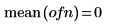
3. ベクトルデータをプロットします。
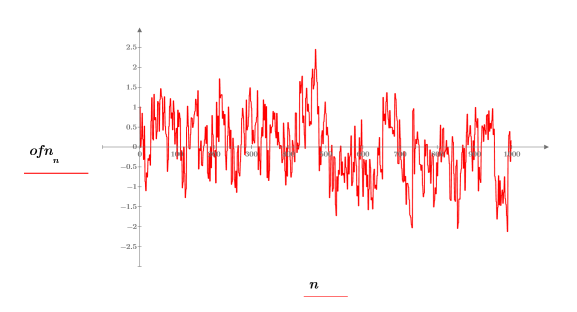
1/f ノイズは、音楽、脳信号、天候、株式市場の動向、その他の階層型干渉システムをはじめとするさまざまな自然現象や人為現象に現れます。たとえば、さまざまなジャンル (ロック、ジャズ、クラシック) の音楽のサンプルをデジタル化すると、それらのパワースペクトルの分布は 1/f ノイズに非常に近いことがわかります。
4. lcorr関数を使用して、このノイズと上記の手順で生成した白色ノイズの自己相関を計算することで、これらの統計的構造を比較します。
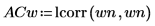
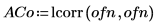
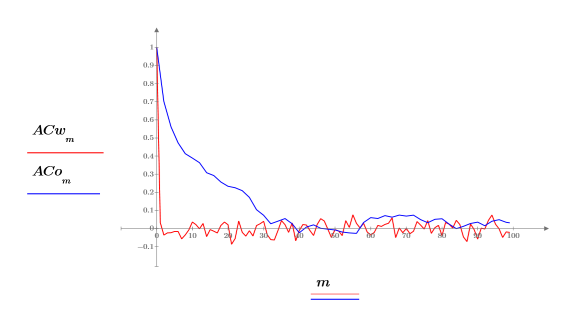
白色ノイズとは異なり、onefn によって生成されたノイズは相関し、ラグが増大するに従って相関は減衰しています。
パワースペクトルを使用したノイズの信号の比較
白色ノイズと 1/f ノイズの違いについて理解するもう 1 つの方法として、これらのノイズのパワースペクトルを比較します。
1. 20 周波数から成る 50 個の区間を定義します。
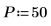
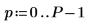
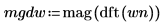
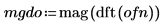
3. 周波数区間平均化することで結果を平滑化します。
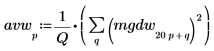
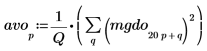
4. 白色ノイズスペクトルをプロットします。
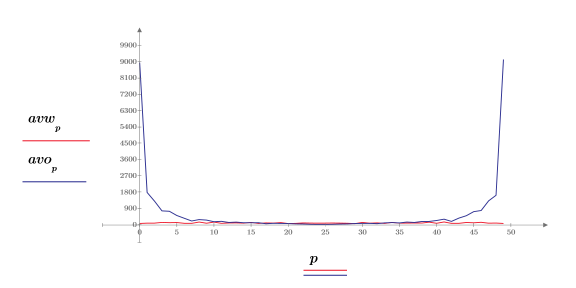
白色ノイズスペクトルは、予想どおり、ほぼ平らになっています。1/f 近似値の大きさのスペクトルは、周波数が大きくなると急激に低下しています。
5. log関数を使用して、よりわかりやすい大きさの対数を計算します。
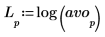
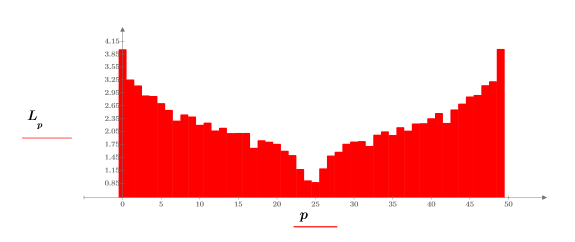
実験
実験として、ランダム位相の 1/f パワースペクトルを作成し、逆変換を行ってノイズベクトルを取得します。
1. スペクトルの幅を定義します。
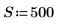
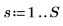
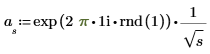
3. 変換の後半を作成します (実際の信号では、後半は中心点を中心とした共役対称になります)。
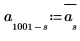
4. ノイズの平均値をゼロに設定します。
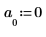
5. idft関数を使用して、逆フーリエ変換 (タイムドメインへの変換) を行います。
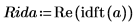
6. 逆変換の実数値をプロットします。
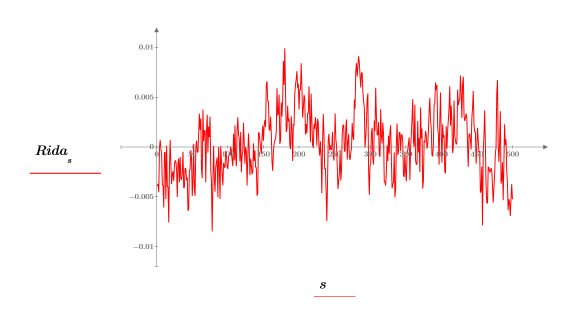
7. lcorr 関数を使用して、自己相関曲線を計算します。
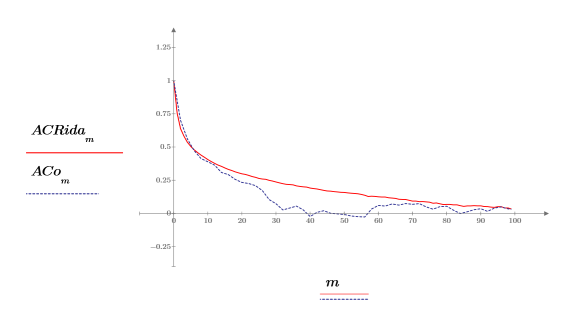
自己相関の振る舞いは onefn からの出力とほぼ同じであり、0 の位置で約 1.0 の相関があり、その他の点での相関度はさまざまです。