例: QR 行列の因子分解

関数 > ベクトルと行列 > 行列の分解 > 例: QR 行列の因子分解

例: QR 行列の因子分解

QR関数を使用して、QR 行列分解を実行します。

• ブール比較実行時の論理不一致を避けるには、「計算オプション」ドロップダウンリストの「近似等価」を有効にします。

• 例では複素行列を入力として使用していますが、関数には入力として実数行列を使用することもできます。

ピボット付き QR 分解

1. 大きさが m x n の実数行列 M1 (m > n) を定義します。

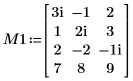
2. 引数 p を設定してピボットの有効化/無効化を制御します。

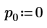
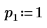
3. QR 関数を使用して、行列 M1 の QR 行列分解を実行します。

デフォルト関数 QR(M1) は QR(M,1). と等価です。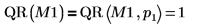

4. M1 x P1 = Q1 x R1 を表示します。

<region id="ID0E6SUFB" actualWidth="167.83666666666665" actualHeight="81.4" top="1209.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="16"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P1</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ENTUFB" actualWidth="165.74" actualHeight="81.4" top="1209.6000000000001" left="211.20000000000005" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="18"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R1</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EAUUFB" actualWidth="153.23666666666668" actualHeight="25.6" top="1286.4" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="20"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P1</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R1</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
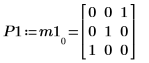
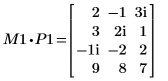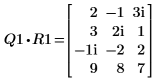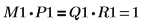関係は論理的に真です。

5. submatrix関数を使用して行列 M2 (m < n) を抽出し、QR 関数を適用します。

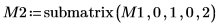
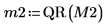
6. M2 x P2 = Q2 x R2 を表示します。

<region id="ID0EN1UFB" actualWidth="69.890000000000015" actualHeight="36.800000000000004" top="1516.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="26"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P2</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m2</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E21UFB" actualWidth="71.38666666666667" actualHeight="36.800000000000004" top="1516.8000000000002" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="28"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">Q2</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m2</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EJ2UFB" actualWidth="70.816666666666677" actualHeight="36.800000000000004" top="1516.8000000000002" left="230.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="30"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">R2</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m2</id> <real>2</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0E32UFB" actualWidth="153.23666666666668" actualHeight="25.6" top="1555.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="32"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M2</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P2</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q2</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R2</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
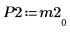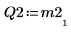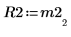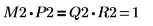関係は論理的に真です。

7. submatrix 関数を使用して行列 M3 (m = n) を抽出し、QR 関数を適用します。

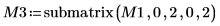
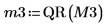
8. M3 x P3 = Q3 x R3 を表示します。

<region id="ID0EBCVFB" actualWidth="69.890000000000015" actualHeight="36.800000000000004" top="1785.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="38"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P3</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m3</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EPCVFB" actualWidth="71.38666666666667" actualHeight="36.800000000000004" top="1785.6000000000004" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="40"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">Q3</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m3</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E4CVFB" actualWidth="70.816666666666677" actualHeight="36.800000000000004" top="1785.6000000000004" left="230.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="42"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">R3</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m3</id> <real>2</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EQDVFB" actualWidth="153.23666666666668" actualHeight="25.6" top="1824.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="44"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M3</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P3</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q3</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R3</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
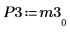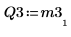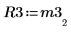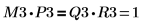関係は論理的に真です。

ピボットなし QR 分解

1. ピボットを無効にしてから QR 関数を行列 M1 (m > n) に適用します。

2. M1 = Q10 x R10 を表示します。

<region id="ID0EDKVFB" actualWidth="140.69333333333333" actualHeight="81.4" top="2380.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="52"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ERKVFB" actualWidth="170.95" actualHeight="81.4" top="2380.8" left="211.20000000000005" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="54"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q10</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R10</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EELVFB" actualWidth="142.05333333333334" actualHeight="25.6" top="2457.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="56"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q10</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R10</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
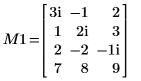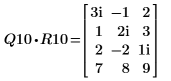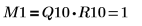関係は論理的に真です。

3. ピボットを無効にしてから QR 関数を行列 M2 (m < n) に適用します。

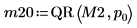
4. M2 = Q20 x R20 を表示します。

<region id="ID0EIQVFB" actualWidth="87.346666666666664" actualHeight="36.800000000000004" top="2649.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="60"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">Q20</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m20</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EWQVFB" actualWidth="86.776666666666671" actualHeight="36.800000000000004" top="2649.6000000000004" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="62"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">R20</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m20</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EJRVFB" actualWidth="142.05333333333334" actualHeight="25.6" top="2688.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="64"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M2</id> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q20</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R20</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
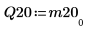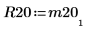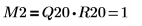関係は論理的に真です。

5. ピボットを無効にしてから QR 関数を行列 M3 (m = n) に適用します。

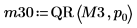
6. M3 = Q30 x R30 を表示します。

<region id="ID0EMWVFB" actualWidth="87.346666666666664" actualHeight="36.800000000000004" top="2880.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="68"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">Q30</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m30</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E1WVFB" actualWidth="86.776666666666671" actualHeight="36.800000000000004" top="2880.0000000000005" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="70"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">R30</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m30</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0ENXVFB" actualWidth="142.05333333333334" actualHeight="25.6" top="2918.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="72"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M3</id> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q30</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R30</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
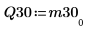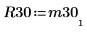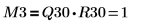関係は論理的に真です。