例: 線形予測法
burg関数とyulew関数を使用して、指定した線形予測モデルの係数を生成します。これらの関数は、それぞれ Burg 法と Yule-Walker アルゴリズムを実行します。これらのアルゴリズムとその背景にある数学的手法については、Sophocles J. Orfanidis 著『Optimum Signal Processing』 (Macmillan ,1989) を参照してください。
Yule-Walker アルゴリズムによる予測
1. cos関数を使用して、余弦信号を定義します。
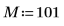
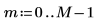
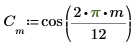
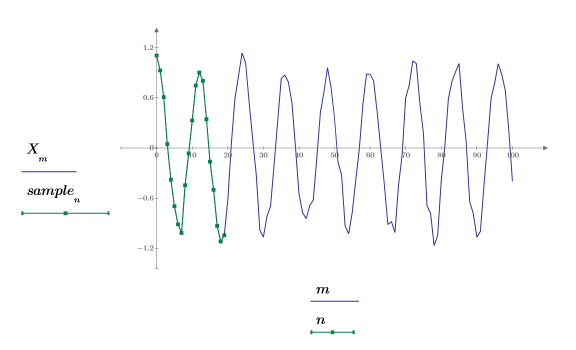
2. 信号をプロットします。
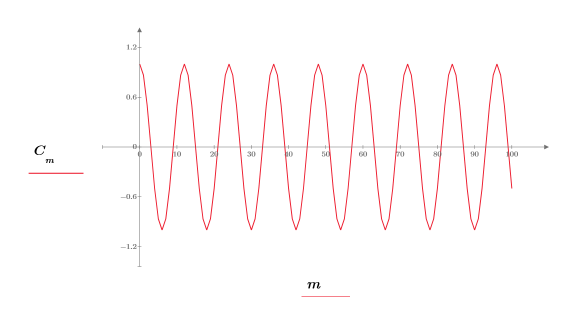
3. rnd関数を使用して、信号にランダムノイズを付加します。
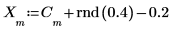
4. 元の信号とノイズを含む信号をプロットします。
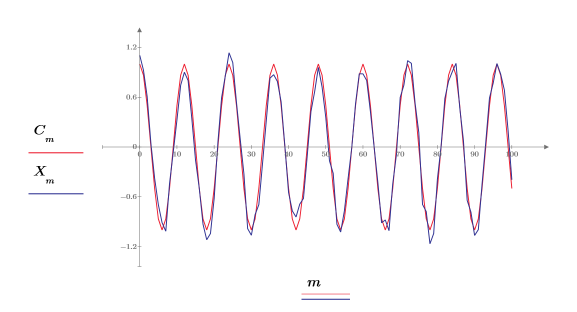
ランダム成分の中心が振幅 0 になるように信号から 0.2 を引いています。
5. 信号の先頭から短いサンプルセットを抽出します。
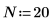
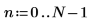
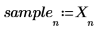
6. 予測の次数を設定し、yulew 関数を使用して係数を計算します。
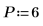
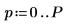

◦ これらの係数は元の信号を近似する全極フィルタに使用します。予想どおり、余弦を表す大きな極が 1 つと、ノイズを近似するいくつかの小さな極があります。
◦ 次数 P によって、シーケンス内の次の値の予測に使用される連続する値の数が決まります。係数ベクトルの 1 番目 から 6 番目の要素が使用され、常に 1 であるゼロ番目の要素は無視されます。この 1 は、y を予測誤差フィルタとして使用してすべての予測誤差を生成する場合に必要になります。
7. 信号内の前の P 個の点を使用して計算された予測点を元のデータと比較します。これによって、信号 X の代わりにこのフィルタを使用するのが適切であるかどうかがわかります。
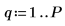
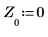
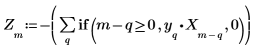
8. 元の信号と予測される信号をプロットします。
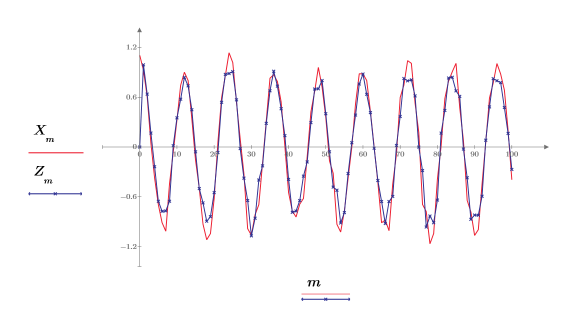
データの最初の 20 個の点だけを使用した場合でも、近似は非常に良好です。
9. response関数を使用して、係数配列をフィルタとして使用し、サンプルを入力として応答を計算することで、Yule-Walker 係数での予測誤差を生成します。
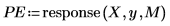
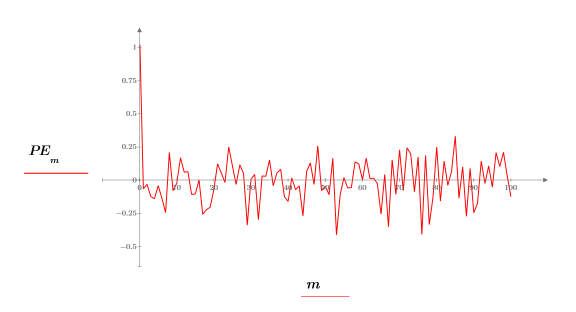
この全係数から成る配列を予測誤差フィルタとも呼びます。
10. これらの誤差によって前の 2 つのプロット間で実際に差が生じていることを確認します。
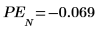
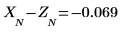
Yule-Walker アルゴリズムでは予測誤差の二乗の和が最小化されます。
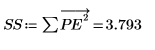
11. y を摂動させて (1 つ目以外のすべての係数に小さなランダム量を加算して) 和を再計算することで最小化を抜き取り検査します (以下の rnd 関数にカーソルを置き、[F5] キーを何回か押します)。
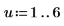
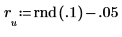
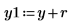
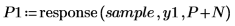
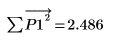
Burg 法による予測
1. 線形予測が十分に機能する、既知の係数を持つ自己相関プロセスシーケンスを作成します。
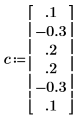
2. 時系列を初期化します。
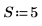
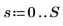
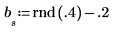
3. 自己回帰とノイズを使用することで残りの時系列を生成します。
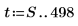
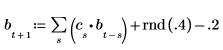
4. 全時系列をサンプルとしてとり、次数 6 のモデルの係数を計算します。次に burg 関数を使用して係数を計算します。
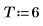
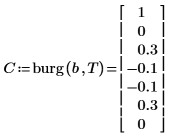
5. このヘルプの符号の規約に従って、実際にプロセスの基になった係数を比較します。
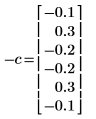
◦ ゼロ番目の係数は常に 0 であるため、除外されています。
◦ 計算された C の要素 1 と 5 は異なります。
6. Burg 法によって計算された係数のベクトル C を使用して予測誤差を生成します。
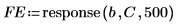
◦ Burg 法では最初の P 個の誤差に 0 の重みが加えられるので、Yule-Walker による最小化と同様に、最小化はサンプルのゼロパディングの影響を受けません。
◦ Burg 法では、前方誤差 FE と後方誤差 BE の両方が考慮されます。
7. 関数 response と reverse を使用して、後方誤差を計算します。
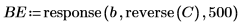
8. 予測誤差 FE と自己回帰関数 b を使用して実際の予測値 AP を計算し、Pth 番目の項から開始する一連の予測値と実際の値の一部をプロットします。
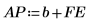
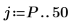
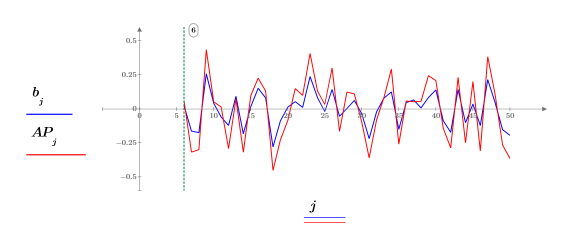
スペクトル推定
線形予測法によって生成された係数を使用して、モデル化するプロセスのパワースペクトルを推定できます。このコンテキストでは Burg アルゴリズムは最大エントロピースペクトル解析 (MESA) と呼ばれ、短い時系列のスペクトルの計算は FFT よりも正確である場合があります。
ガウスノイズが付加された正弦曲線の和から成るプロセスのパワースペクトルを推定します。
1. sin関数を使用して、正弦成分が 2 つある信号を定義します。
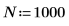
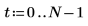
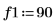
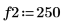
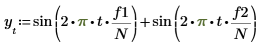
2. gaussn関数を使用して、ガウスノイズを付加します。
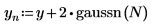
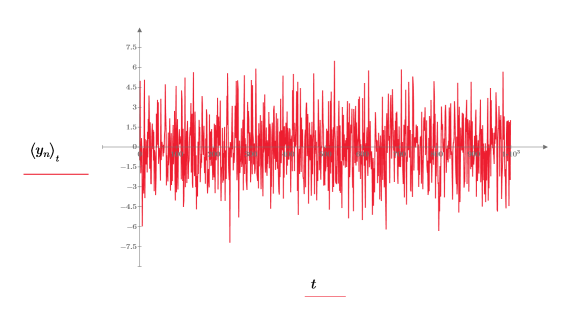
gaussn 関数は、平均値 0、標準偏差 1 のガウス確率分布に従う n 成分の乱数ベクトルを返します。
3. 線形予測の次数を 2 つ定義します。
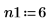
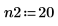
4. burg 関数を使用し、サンプルとして全時系列を使用して、2 つの次数の自己回帰モデルのスペクトルを推定します。
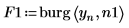
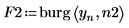
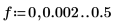
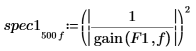
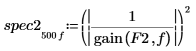
6. 2 つのパワースペクトルをプロットします。
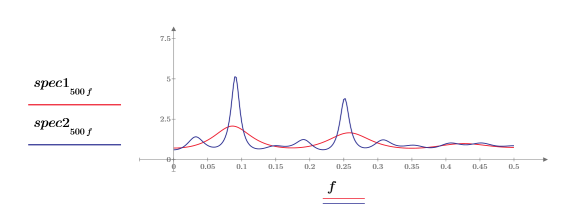
◦ 各パワースペクトルには、2 つのピークがあります。
◦ どちらのスペクトルでも、高い方と低い法の周波数ピークがほぼ同じ周波数で発生しています。
7. ゲインピークとその発生周波数を求めるために、spec1 曲線と spec2 曲線をそれぞれ 2 つのセグメントに分割します。
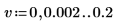 | 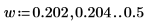 |
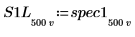 | 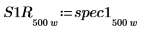 |
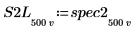 | 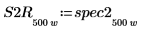 |
8. if 関数を使用して、特定のセグメントがピークとなる周波数を返す関数を定義し、これを使用して各スペクトルトレースの左側および右側のピークを求めます。
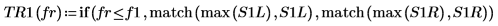 | |
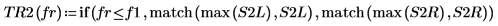 | |
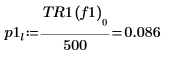 | 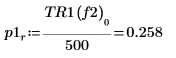 |
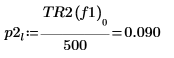 | 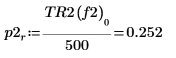 |
9. max関数を使用して、それぞれのピークのマグニチュードを計算します。
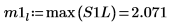 | 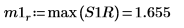 |
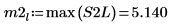 | 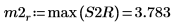 |
10. それぞれの関数を個別にプロットします。横マーカーと縦マーカーを使用して、各ピークのマグニチュードとその発生周波数を示します。
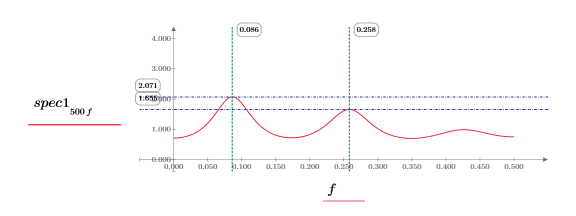
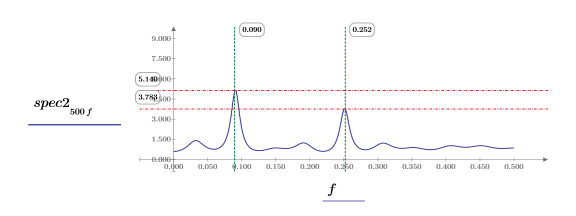
◦ ワークシートの再計算中に、2 つのプロットを確認します。
◦ 再計算ごとにピークのマグニチュードが異なり、通常はさまざまな値をとります。ただし、マグニチュードが等しくなる可能性もあります。
◦ ピークはほぼ同じ周波数で発生します。
この方法によるスペクトル推定の詳細については、S. Lawrence Marple, Jr. 著 Digital Spectral Analysis with Applications (Prentice-Hall, Inc) を参照してください。