例: 補間とサンプリング
デフォルトの FIR フィルタでの multirate 関数
multirate 関数は、線形位相 FIR フィルタのグループ遅延を利用して、初期出力の遷移が終了する場所を推定してそこで打ち切ります。
1. 信号のパラメータを定義します。
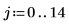 |
|
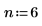 |
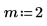 |
2. sin関数を使用して、正弦和信号を定義します。
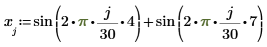
3. この信号に multirate 関数を適用します。
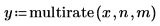
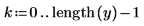
4. 再サンプリングした信号をプロットします。
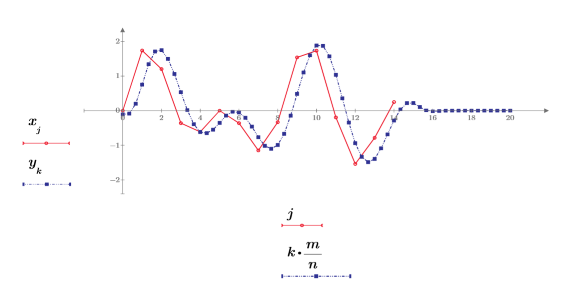
プロットから、再サンプリングした信号はわずかにシフトし、元のデータ点の n/m 倍の数のデータ点があることがわかります。このシフトは FIR フィルタによって生じ、そのグループ遅延と同じです。
オプションのローパス FIR フィルタでの multirate 関数
1. カットオフ周波数、係数の数、逓減ウィンドウのタイプを定義します。
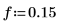 | 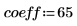 | 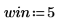 |
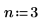 | 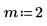 |
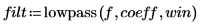
3. multirate 関数を使用して、別の係数で信号 x を再サンプリングします。
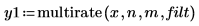
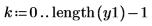
4. 再サンプリングした信号をプロットします。
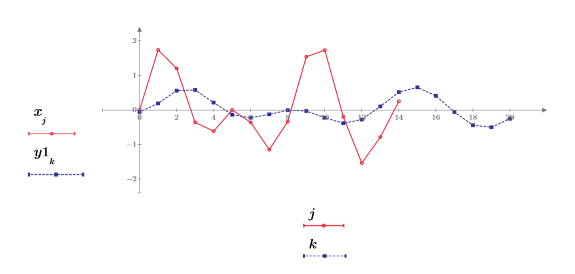
FIR フィルタはアップサンプリングレート n と等しいゲインを持たないので、再サンプリングによって信号が減衰しています。
5. FIR フィルタの係数を調整してゲインを修正し、再サンプリングした信号を再プロットします。
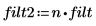
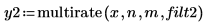
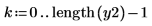
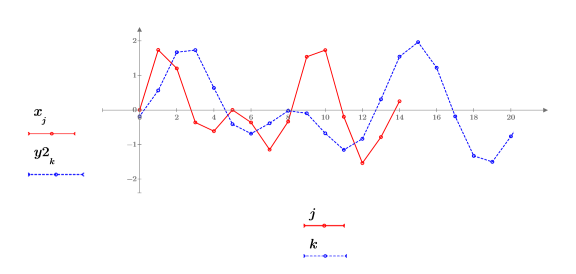
FIR フィルタの係数を調整すると、尺度化の効果が失われます。
信号のアップサンプリング
multirate 関数を使用して、信号をアップサンプリングまたはダウンサンプリングできます。
1. multirate 関数を使用し、n/m 比率を上げることで信号 x をアップサンプリングします。
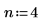 | 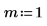 |
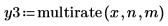 | |
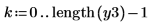 |
2. アップサンプリングした信号をプロットします。
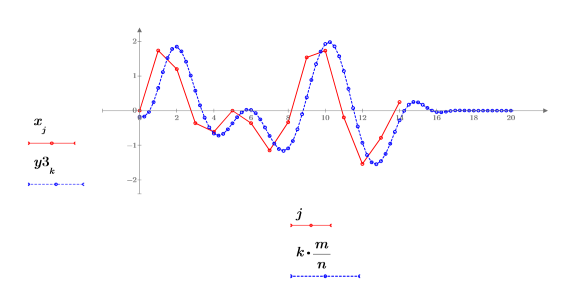
長さの値からわかるように、n/m 比を大きくしたことでサンプルの総数が増え、元の信号の連続する任意の 2 つのサンプル間の新しいサンプルの数が増えました。
3. multirate 関数を使用し、x 比率を下げることで信号 n/m をダウンサンプリングします。
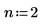 | 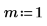 |
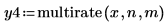 | |
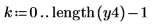 |
4. ダウンサンプリングした信号をプロットします。
長さの値からわかるように、n/m 比を小さくしたことでサンプルの総数が減り、元の信号の連続する任意の 2 つのサンプル間の新しいサンプルの数が減りました。
データのアップサンプリング
upsample 関数は、元のデータに対して FFT を実行します。このとき、必要な補間長さの変換を作成するために係数範囲の中央にゼロを追加します。この後、この関数は拡張後のスペクトルを逆変換します。データを補間するのに決まった方法はありません。特別に設計された FIR フィルタを使用することもできます。規則的な振る舞いのデータでは、この関数は妥当な補間を返します。
1. 補間係数 n を設定し、upsample 関数を信号 x に適用します。
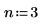
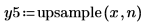
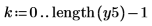
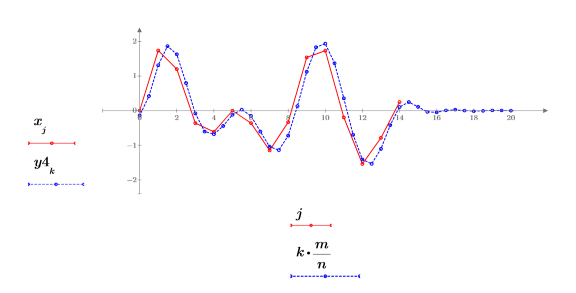
2. 返された信号をプロットします。
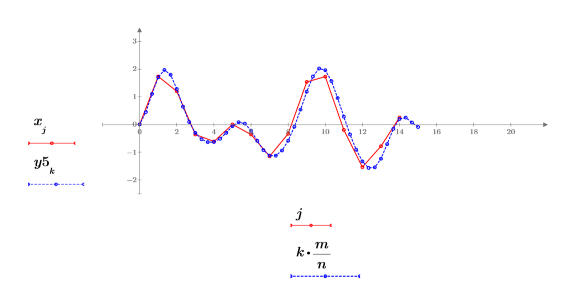
返された信号は、信号 x を元のデータ点の n 倍の点で補間したものです。
信号の再サンプリング
resample 関数は、上記のように補間を使用して元のデータ点の n 倍の点を生成し、mth 番目ごとの点から成る出力を生成します。
1. デシメーション係数 m と補間係数 n を設定します。
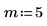 | 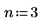 |
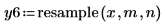 | |
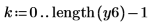 |
2. 返された信号をプロットします。
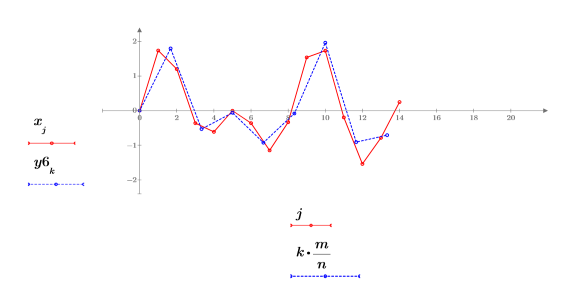
返された信号の点の数は元のデータ点の 3/5 なので、サンプルの間隔は元の間隔の 5/3 になります。
非周期的入力と周期的入力でのアップサンプリングの使用
upsample 関数は、入力が周期的であることを前提としています。両方の場合で返される信号を調べます。
非周期的入力
1. 補間係数を設定します。
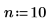
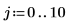
2. 非周期的入力信号を定義します。
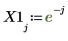
3. upsample 関数を適用します。
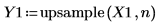
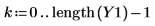
4. 返された信号をプロットします。
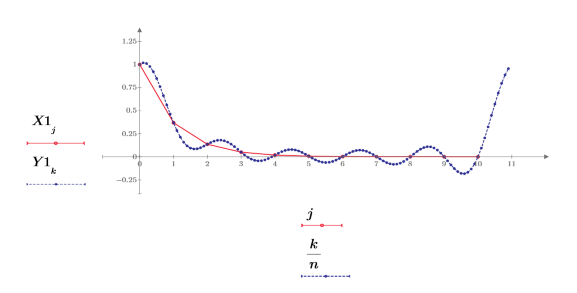
補間ルーチンは X が周期的であることを前提としています。したがって、グラフの終端付近では、最初の高さ 1 に戻るように点が補間されます。ただし、入力シーケンスを折り返したときにある程度滑らかな関数が得られる場合、この関数は実用的な結果を返します。
周期的入力
1. 補間係数を設定します。
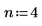
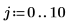
2. 周期的入力信号を定義します。
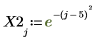
3. upsample 関数を適用します。
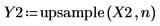
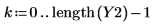
4. 返された信号をプロットします。
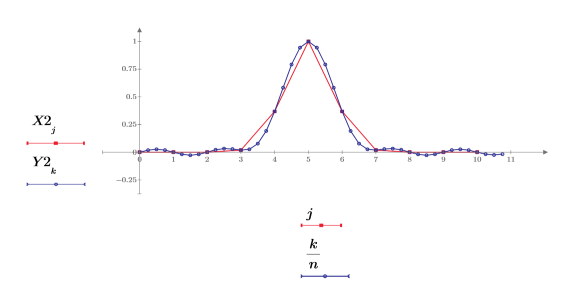
元の信号が周期的である場合、補間によって元の信号により近い近似値が求められます。