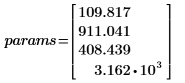例: 勾配演算子
• 関数 f を定義します。
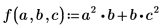
勾配演算子を使用して、f の偏微分のベクトルを取得します。
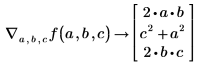
• ベクトル関数を定義し、ベクトル x による関数 f の勾配を計算します。
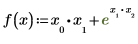

この例では、すべての配列の最初の添字を設定するORIGINは 0 に設定されています。
f で最も大きい下付き文字がついている変数は x2 です。Mathcad は、3 つの変数 x0、x1、および x2 があることを前提としています。結果は、これらの変数の偏微分を含む 3 つの値の勾配ベクトルです。x0 または x1 が f に表示されなかった場合、Mathcad は 3 つの値のベクトルを返しますが、欠落している変数に対応するエントリは 0 に設定されます。
f に表示される最も大きい下付き文字 n の場合、Mathcad は n + 1 の変数は x0、 x1、... xn であると仮定し、長さ n + 1 のベクトルを返します。
• x を数値的に定義する場合、等号 = で勾配を評価できます。Mathcad は、x の値で勾配を評価し、点 x での勾配を表す数字のベクトルを返します。x の長さは f に表示される最も大きい下付き文字より大きくなければならず、Mathcad は length(x) エントリがある勾配を返します。
次の例では、x0 と x1 のみが式に表示される変数で、Mathcad は x0 と x1 についての偏微分を取得し、2 つの値のベクトルを返します。
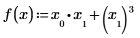
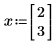
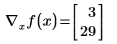
ただし、x を 3 成分ベクトルとして定義する場合、Mathcad は式に表示されない追加の変数 x2 が存在すると仮定します。結果は 3 成分のベクトルです。
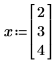
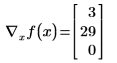
genfit 関数での勾配演算子の使用
勾配演算子は、一般的な非線形関数をデータセットに適合させる genfit 関数の引数を設定するときに特に便利です。
• 次の表のデータを使用します。
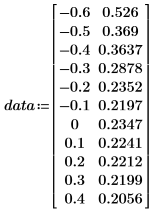
• 1 列目にはデータの x 値が含まれており、2 列目には y 値が含まれています。
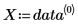
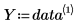
• 次の形式の関数によってデータをモデル化します。
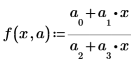
ここで、a1、a2、および a3 は、ベクトル a に含まれている未知のパラメータです。
次のように genfit を呼び出してデータをモデル化できます。
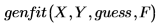
この式では
◦ X と Y は、データの x 値と y 値が含まれているベクトルです。
◦ guess は、パラメータの初期推定値のベクトルです。
◦ F は、1 つ目のエントリがモデル関数 f(x, a) であり、残りのエントリが未知のパラメータについての f の偏微分であるベクトルです。
• 勾配演算子と stack 関数を使用してベクトル F を作成します。
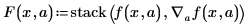

• stack 関数は、勾配演算子によって作成された偏微分ベクトルの上にモデル関数 f を配置します。
• 次に、パラメータの推定値ベクトルを作成します。
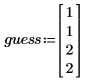
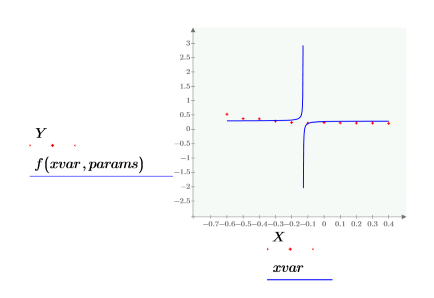
• 次のように genfit を適用します。
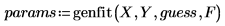
• 最良適合を提供するパラメータは次のとおりです。