例: 順変換 dft
dft関数を使用して、一定時間間隔または一定距離間隔でサンプリングした、任意の大きさの実数または複素数のベクトルまたは行列の複素フーリエ変換を求めます。
1D 複素正弦波データ
間隔 T で N 個のサンプルデータ点から成る複素データセットを作成します。
1. データ点の数を定義します。
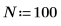
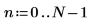
2. サンプルを収集する時間 T を定義します。
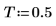
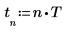
3. 角周波数を設定します。
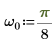
4. exp関数を使用して指数関数を定義します。
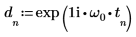
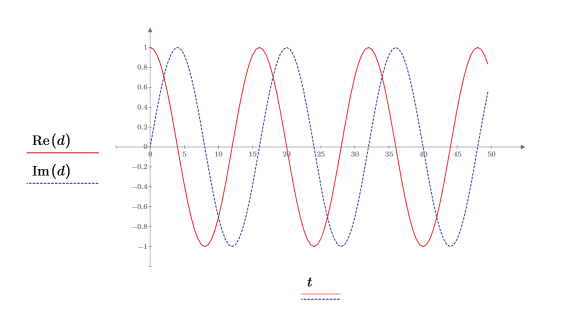
6. dft 関数を適用して、データを周波数領域に変換します。
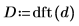
7. D の絶対値を新しい配列に格納します。
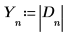
8. サンプリング周波数、および変換後のベクトルの n 番目のエントリに相当する周波数を定義します。
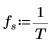
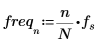
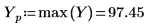
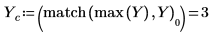
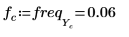
10. 変換したベクトルをプロットし、縦マーカーと横マーカーを使用して振幅が最大になる周波数にマーク付けします。
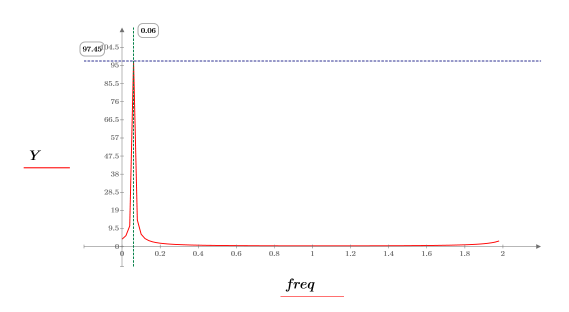
◦ 周波数領域のサンプルの上半分は負の周波数を示します。
◦ この複素信号には負の周波数情報はありません。
その他の情報
• 実数データのベクトル v の場合、ベクトル dft(v) は、通常、中央値から共役対称である複素ベクトルになります。実数行列の場合、結果の各列は共役対称になります。
• 正方配列入力 A の場合、dft(A) は対称になります。
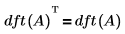
• ナイキストのサンプリング定理によれば、サンプリング周波数はフーリエ変換によって分解する最大周波数の 2 倍以上でなければなりません。
• データ点の数が大きな素数の場合、高速フーリエ変換で使用される素因数アルゴリズムの速度が低下します。この問題が一度も発生することはないかもしれませんが、データ点の数が非常に大きな素数の場合にはこのことを念頭におくようにしてください。