例: 固有ベクトルと固有値
eigenvals、eigenvecs、eigenvec関数を使用して、実数行列または複素行列の固有値と固有ベクトルを求めます。正方行列 M で、以下の式を満たす数値 λ が存在する場合、ゼロ以外のベクトル v が M の固有ベクトルであるという理論を確認します。
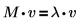
1. 入力正方行列を定義します。
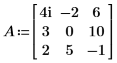
2. eigenvals と eigenvecs を呼び出して、行列 A の固有値と固有ベクトルを求めます。
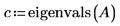
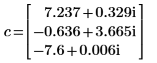
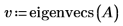

v の最初の列は、c の最初の要素に対応する固有ベクトルです。同様に、v の 2 列目は c の 2 番目の要素に対応する固有ベクトルであり、3 列目以降も同様です。
3. v1 を A の最初の固有ベクトル、c1 を最初の固有値として定義します。A x v1 と c1 x v1 を比較します。
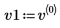
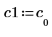
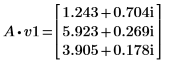 | 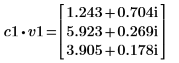 |
4. v2 を A の最初の固有ベクトル、c2 を最初の固有値として定義します。A x v2 と c2 x v2 を比較します。
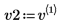
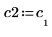
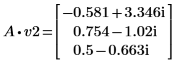 | 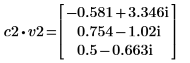 |
5. v3 を A の最初の固有ベクトル、c3 を最初の固有値として定義します。A x v3 と c3 x v3 を比較します。
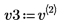
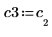
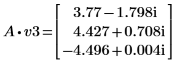 | 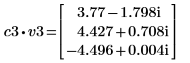 |
6. eigenvec 関数を呼び出して、特定の固有値に対する固有ベクトルを 1 つ返します。
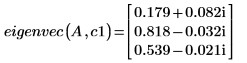

eigenvec と eigenvecs によって返される結果は、必ずしも一致しませんが、どちらも有効な解です。固有ベクトルは一意ではありません。その他の固有ベクトルとはスケール係数を介して関連付けられています。ある固有値に対して、無限の数の固有ベクトルが存在します。