例: 3 次スプライン補間

lspline、pspline、cspline関数を使用して、3 次スプライン (区分的多項式) を作成し、データ点を補間します。

1. 行列を定義します。

2. csort関数を使用して、Cu の 2 番目の列が昇順になるようにデータを並べ替えます。

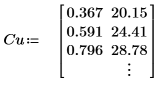
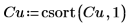
スプライン関数に渡す x の値は昇順でなければなりません。

3. x と y のデータを格納するベクトルを作成します。

4. cspline 関数を使用して 3 次スプラインベクトルを作成してから、interp関数を使用して補間値を取得します。

<region id="ID0EY46T" actualWidth="201.67333333333335" actualHeight="25.6" top="499.20000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="146">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">fitc</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">interp</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">vx</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">vy</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

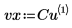
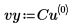
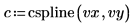
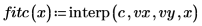
5. lspline 関数を使用して線形スプラインベクトルを作成してから、interp 関数を使用して補間値を取得します。

<region id="ID0E466T" actualWidth="197.04000000000002" actualHeight="25.6" top="633.60000000000014" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="150">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">fitl</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">interp</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">l</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">vx</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">vy</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

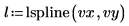
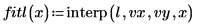
6. pspline 関数を使用して 2 次スプラインベクトルを作成してから、interp 関数を使用して補間値を取得します。

<region id="ID0EDCAU" actualWidth="204.9" actualHeight="25.6" top="768.00000000000011" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="154">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">fitp</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">interp</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">p</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">vx</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">vy</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

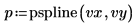
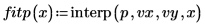
7. 元のデータ点と 3 次スプラインをプロットします。

<region id="ID0EPEAU" actualWidth="576.307692307692" actualHeight="273.6" top="883.20000000000016" left="38.400000000000006" height="273.6" width="576.307692307692" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="160">
          <traceStyle color="#FF00008B" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="161">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Dot">lines</traceStyle>
        </trace>
        <trace resultRef="162">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dot">lines</traceStyle>
        </trace>
        <trace resultRef="163">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Dot">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="441.907692307692" height="196.8" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="20" end="100">
          <axisLine position="origin" positionticmark="0" legendWidth="110.06" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="168">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">vx</id>
              </math>
              <math resultRef="169">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="170">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math resultRef="171">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="165">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </startValue>
            <endValue resultRef="167">
              <real xmlns="http://schemas.mathsoft.com/math50">100</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="10">
          <axisLine position="left" positionticmark="-1" legendWidth="101.72" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="178">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">vy</id>
              </math>
              <math resultRef="179">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="180">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">fitl</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math resultRef="181">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="182">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">fitp</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math resultRef="183">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="184">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">fitc</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math resultRef="185">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="173">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="175">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="177">
              <real xmlns="http://schemas.mathsoft.com/math50">10</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

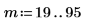
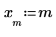
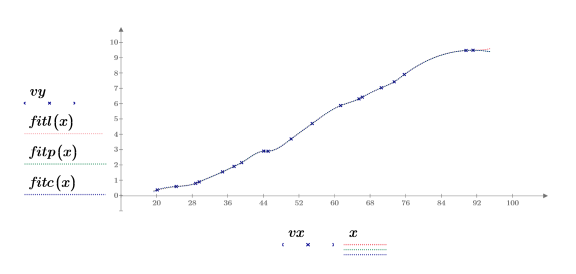
8. 最初の 2 つのデータ点にズームインします。

<region id="ID0E2GAU" actualWidth="576.384615384615" actualHeight="311.6" top="1248.0000000000002" left="38.400000000000006" height="311.6" width="576.384615384615" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="207">
          <traceStyle color="#FF000000" symbol="rectangle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="208">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="209">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="210">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="441.984615384615" height="234.8" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="19" end="25">
          <axisLine position="ticknumberlock" positionticmark="0" legendWidth="110.06" />
          <axisGrid>
            <gridFrequency>7</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="211" display="true" color="#FF000000" value="20.15">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">vx</id>
                <real>0</real>
              </apply>
            </marker>
            <marker display="true" color="#FF000000" value="24.41" />
          </markers>
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="219">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">vx</id>
              </math>
              <math resultRef="220">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="221">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math resultRef="222">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="214">
              <real xmlns="http://schemas.mathsoft.com/math50">19</real>
            </startValue>
            <secondTickValue resultRef="216">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </secondTickValue>
            <endValue resultRef="218">
              <real xmlns="http://schemas.mathsoft.com/math50">25</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.7">
          <axisLine position="ticknumberlock" positionticmark="0" legendWidth="101.72" />
          <axisGrid>
            <gridFrequency>8</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="229">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">vy</id>
              </math>
              <math resultRef="230">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="231">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">fitl</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math resultRef="232">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="233">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">fitp</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math resultRef="234">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="235">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">fitc</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math resultRef="236">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="224">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="226">
              <real xmlns="http://schemas.mathsoft.com/math50">0.1</real>
            </secondTickValue>
            <endValue resultRef="228">
              <real xmlns="http://schemas.mathsoft.com/math50">0.7</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

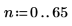
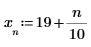
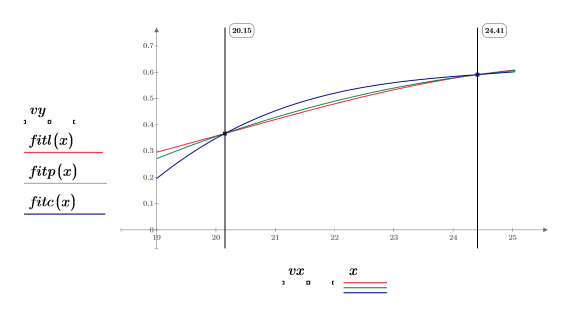
終点以外の結果は 3 つのスプライン関数で同じです。

9. 補間線形スプラインベクトルの 2 次微分係数を計算し、終点で 0 になることを示します。

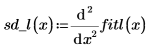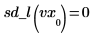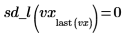10. 補間 2 次スプラインの 2 次微分係数を計算し、終点ではすぐ隣の点の値と等しくなることを示します。

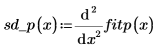
◦ 最初の点と 2 番目の点で 2 次微分係数を評価し、両方が等しくなることを示します。

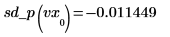
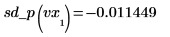
◦ 2 番目から最後までの点と最後の点で 2 次微分係数を評価し、両方が等しくなることを示します。

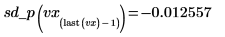
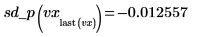
スプライン適合の微分係数を使用して、補間曲線の極大と極小、傾き、その他の特性を求めることができます。