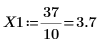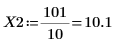例: 2 次のベッセル関数

関数 > 特殊関数 > ベッセル関数 > 例: 2 次のベッセル関数

例: 2 次のベッセル関数

関数Y0、Y1およびYnの関係を表します。関数とその尺度化された型との関係も表示します。

1. 2 つのレンジ変数を次のように定義します。

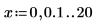
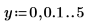
2. 関数 Y0 と Y1 をプロットします。2 次関数 Yn をプロットに次のように追加します。

<region id="ID0E1G16" actualWidth="594.82646715823216" actualHeight="316.8" top="134.40000000000003" left="0" height="316.8" width="594.82646715823216" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="47">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="48">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="49">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="441.226467158232" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="2" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-1" end="1">
          <axisLine position="origin" positionticmark="0" legendWidth="117.44" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Y0</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Y1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">Yn</id>
                  <sequence>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="50">
              <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
            </startValue>
            <secondTickValue resultRef="51">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </secondTickValue>
            <endValue resultRef="52">
              <real xmlns="http://schemas.mathsoft.com/math50">0.75</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

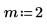
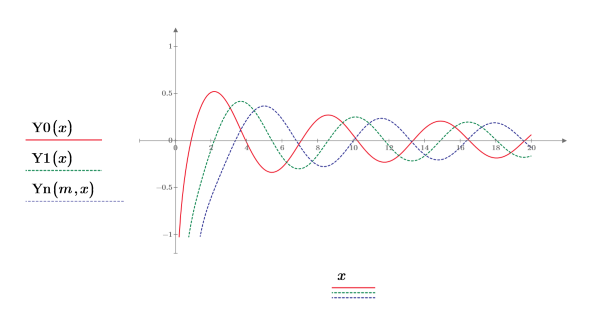
3. 次を示すプロットを作成します。Y0(y)=Yn(0,y)目盛の値をリセットして、X 軸を拡大してより詳細に表示します。

<region id="ID0EOI16" actualWidth="594.826467158232" actualHeight="297.6" top="518.40000000000009" left="0" height="297.6" width="594.826467158232" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="53">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="54">
          <traceStyle color="#FF068149" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="441.226467158232" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="5">
          <axisLine position="origin" positionticmark="2" legendWidth="60.74" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="0.75">
          <axisLine position="origin" positionticmark="0" legendWidth="111.576666666667" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Y0</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Yn</id>
                  <sequence>
                    <real>0</real>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="55">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="56">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.25</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

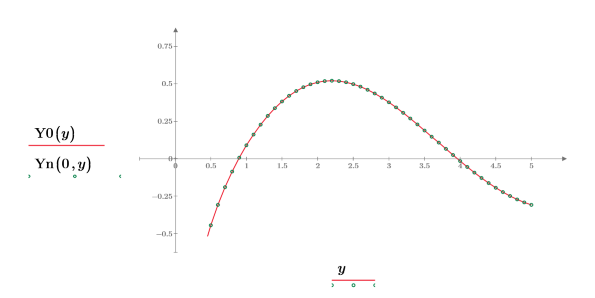
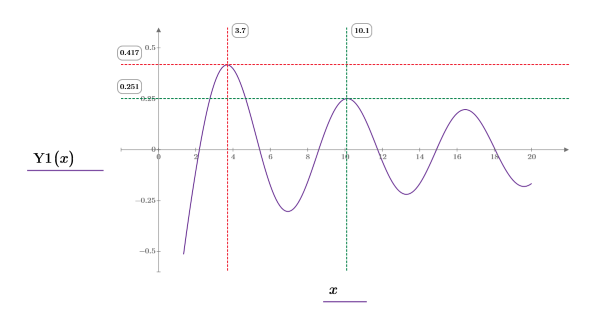
4. 次を示すプロットを作成します。Y1(y)=Yn(1,y)目盛の値をリセットして、X 軸を拡大してより詳細に表示します。

<region id="ID0ECK16" actualWidth="594.82646715823216" actualHeight="297.6" top="864.00000000000011" left="0" height="297.6" width="594.82646715823216" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="57">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="58">
          <traceStyle color="#FF2E3192" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="441.226467158232" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="5">
          <axisLine position="origin" positionticmark="2" legendWidth="60.74" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="0.5">
          <axisLine position="origin" positionticmark="0" legendWidth="111.576666666667" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Y1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Yn</id>
                  <sequence>
                    <real>1</real>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="59">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="60">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.25</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

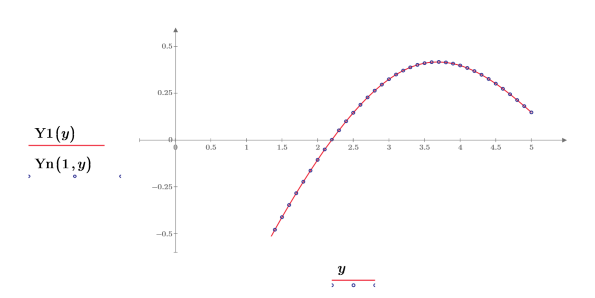
5. シンボリック評価を使用して、2 次のベッセル関数とその尺度化された型の関係を次のように表示します。

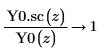
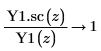
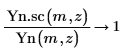
6. 次を示すプロットを作成します。

<region id="ID0EMO16" actualWidth="595.97383557928492" actualHeight="297.6" top="1324.8000000000002" left="0" height="297.6" width="595.97383557928492" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="65">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="66">
          <traceStyle color="#FF662D91" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="442.373835579285" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="5">
          <axisLine position="origin" positionticmark="2" legendWidth="60.74" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="0.75">
          <axisLine position="origin" positionticmark="0" legendWidth="112.636666666667" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Y0</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Y0.sc</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="67">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="68">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.25</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

7. Y1 の最初の 2 つのピークの座標を計算します。関数augmentおよびlocalmaxを使用して、指定した範囲内にあるピークを特定します。

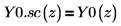
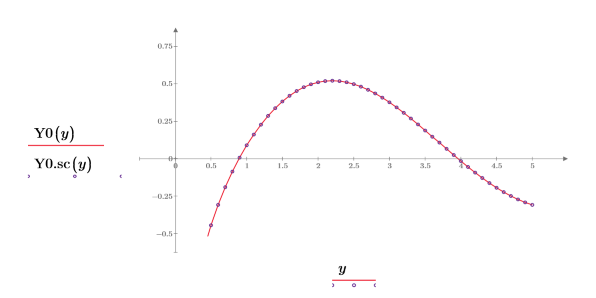
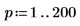
第 2 種ベッセル関数は 0 では定義されません。

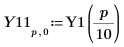
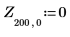
関数 localmax には 2 列の入力行列が必要です。関数 augment を使用してこのような行列を作成します。

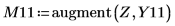
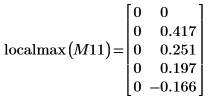
関数は 0 において定義されていないので、(0, 0) における最初の局所最大値は無視できます。

8. 関数matchを使用して、ピークが発生している横方向の値を求めます。最も正確な結果を得るためには、TOL の値を小さくします。

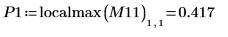
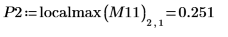
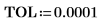
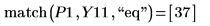
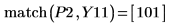
9. プロットにマーカーを追加して、最初の 2 つのピークをマーク付けします。

レンジ変数のステップは 0.1 です。これは、関数 match で識別される要素の添字の 1/10、つまり 3.7 と 10.1 でそれぞれピークが発生することを示します。

<region id="ID0ED116" actualWidth="596.7843618950742" actualHeight="316.79999999999995" top="2208.0000000000005" left="0" height="316.79999999999995" width="596.7843618950742" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="81">
          <traceStyle color="#FF662D91" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="462.384361895074" height="259.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="2" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="82" display="true" color="#FFED1D2F" line-style="Dash" value="3.7">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">X1</id>
            </marker>
            <marker resultRef="83" display="true" color="#FF068149" line-style="Dash" value="10.1">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">X2</id>
            </marker>
          </markers>
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="0.5">
          <axisLine position="origin" positionticmark="0" legendWidth="94.9333333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="84" display="true" color="#FFED1D2F" line-style="Dash" value="0.41667437268380769">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">P1</id>
            </marker>
            <marker resultRef="85" display="true" color="#FF068149" line-style="Dash" value="0.25084443625651331">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">P2</id>
            </marker>
          </markers>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Y1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="86">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="87">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.25</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>