例:エアリー関数
1. シンボリック評価を使用して、関数 DAi が関数 Ai の 1 次導関数であること、および関数 DBi が関数 Bi の 1 次導関数であることを次のように示します。
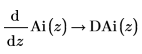
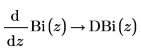
2. 横方向のレンジ変数を定義して、関数 Ai と Bi を次のようにプロットします。
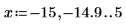
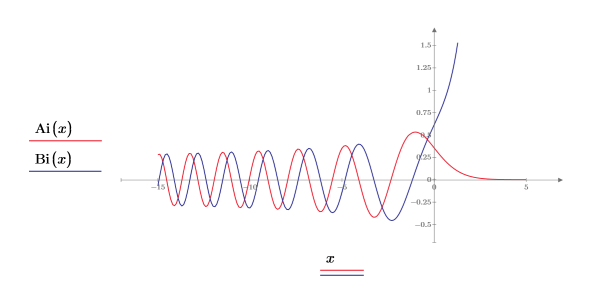
位相は異なりますが、2 つの関数は -x が X 軸に沿って 0 に近づくにつれて分かれ始めるまではよく似ています。
3. ベクトル Z1 と Z2 を、Ai と Bi を使用して次のように定義します。
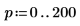
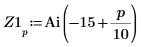
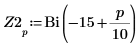
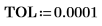
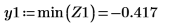
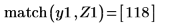
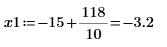
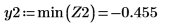
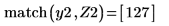
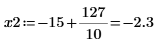
5. 垂直マーカーを追加して、関数が分岐を始める直前の極小値を表示します。
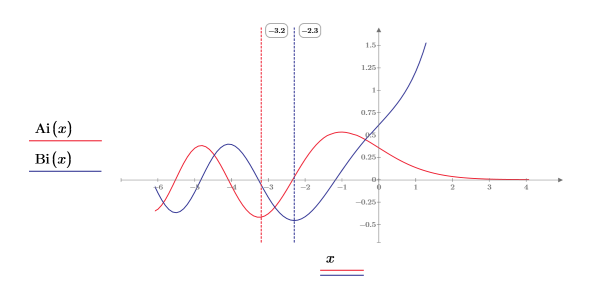
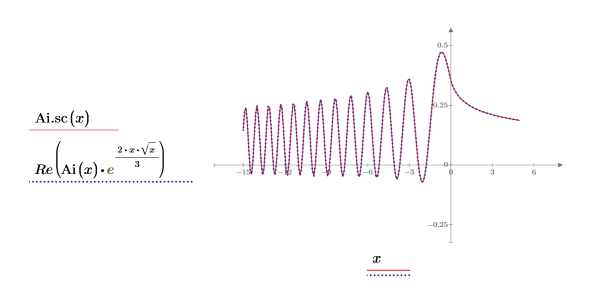
6. シンボリック評価を使用して、各関数とその尺度化された型の関係を次のように表示します。
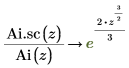
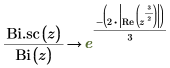
7. 次を示すプロットを作成します。
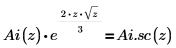
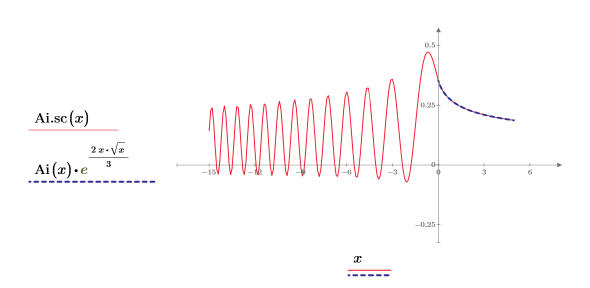
2 つ目のトレースには x の負の値で複素数値があります。
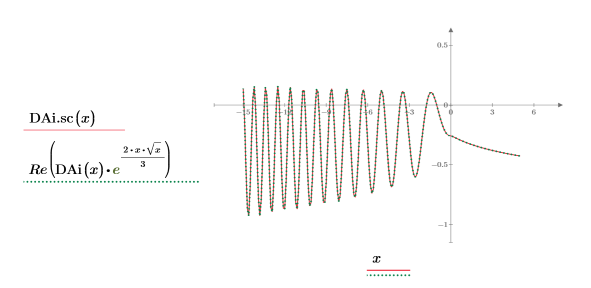
8. 前述のプロットを再度作成して、2 つ目のトレースの実数値を次のように示します。
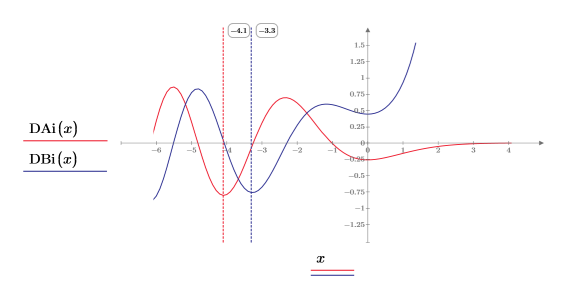
9. 関数 DAi と DBi を次のようにプロットします。
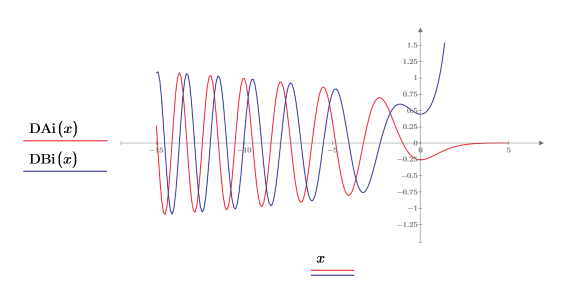
位相は異なりますが、2 つの関数は -x が X 軸に沿って 0 に近づくにつれて分かれ始めるまではよく似ています。
10. DAi と DBi をベクトル Z11 と Z21 にそれぞれ保存します。
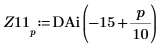
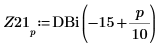
11. 0 に最も近い DAi と DBi の局所最小値の座標を求めます。
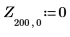
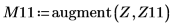
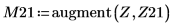

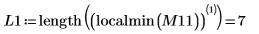
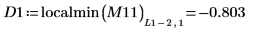

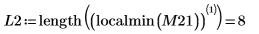
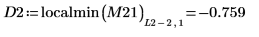
12. DAi と DBi の極小値に一致する座標を求めます。
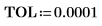
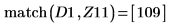
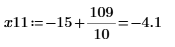
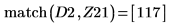
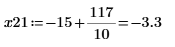
13. 垂直マーカーを追加して、関数が分岐を始める直前の極小値を表示します。
14. シンボリック評価を使用して、各関数とその尺度化された型の関係を次のように表示します。
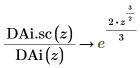
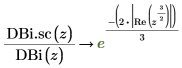
15. 次を示すプロットを作成します。
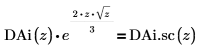
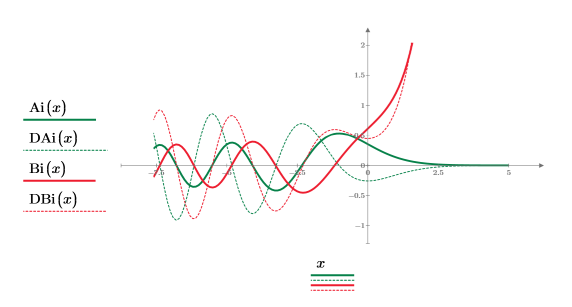
16. 関数 Ai、DAi、Bi、および DBi を同じグラフにプロットして比較します。