Integral Operator
|
Operator
|
Description
|
Keyboard Shortcut
|
|---|---|---|
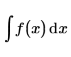 |
Returns the indefinite integral of f(x).
|
Ctrl+Shift+I
|
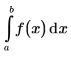 |
Returns the definite integral of f(x) from a to b.
|
Watch this video to learn more about solving definite integrals:
Operands
• f is any scalar-valued function. When calculating the definite integral f must be defined in the closed interval [a, b]. The function can be complex, except in the case of infinite limit integration. It can be a function of any number of variables.
• x is the variable of integration.
• a, b are real scalars. They must have units compatible with x.
Additional Information
• You can create multiple integrals by inserting the integral operator multiple times.
• Sharply peaked integrands, discontinuous integrands, or integrands whose shape is not readily characterized by a single length scale may not evaluate accurately. You can integrate such functions by parts.
• This operator may also be evaluated symbolically for integrals with a closed-form solution.
• You can choose a solving algorithm for definite integrals. Read more about choice of solving algorithms here.