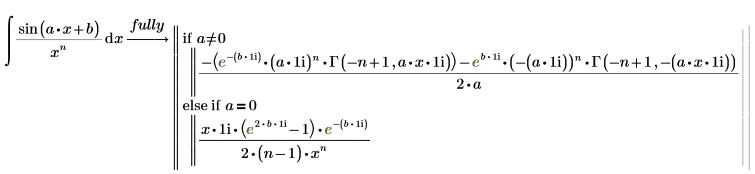Example: Symbolic Integral Functions Using the Keyword fully

Symbolics > Working with Symbolics > Calculus > Example: Symbolic Integral Functions Using the Keyword fully

Use the keyword fully to receive a full detailed solution to a symbolic function. Using fully, you can receive solutions for different values of the function’s coefficients. In the following example: a, b, and c. To narrow the solution to only one value of the function’s coefficients, use the assume keyword.

1. Evaluate a symbolic integral.

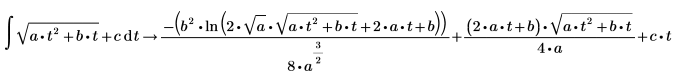
2. Evaluate the full conditioned solution of the integral, using the keyword fully.

<region id="ID0ECZPMB" width="742.40400125185647" actualWidth="742.40400125185647" actualHeight="239.90586691422462" top="172.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="14">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t</id>
          </boundVars>
          <apply>
            <plus />
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <plus />
                <apply>
                  <mult />
                  <id xml:space="preserve">a</id>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                    <real>2</real>
                  </apply>
                </apply>
                <apply>
                  <mult />
                  <id xml:space="preserve">b</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                </apply>
              </apply>
            </apply>
            <id xml:space="preserve">c</id>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <id xml:space="preserve">fully</id>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <notEqual />
                <id xml:space="preserve" labels="VARIABLE">a</id>
                <real>0</real>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <plus />
                  <apply>
                    <div />
                    <apply>
                      <neg />
                      <parens>
                        <apply>
                          <mult />
                          <apply>
                            <pow />
                            <id xml:space="preserve" labels="VARIABLE">b</id>
                            <real>2</real>
                          </apply>
                          <apply>
                            <id xml:space="preserve" labels="FUNCTION">ln</id>
                            <apply>
                              <plus />
                              <apply>
                                <mult />
                                <apply>
                                  <mult />
                                  <real>2</real>
                                  <apply>
                                    <nthRoot />
                                    <placeholder />
                                    <id xml:space="preserve" labels="VARIABLE">a</id>
                                  </apply>
                                </apply>
                                <apply>
                                  <nthRoot />
                                  <placeholder />
                                  <apply>
                                    <plus />
                                    <apply>
                                      <mult />
                                      <id xml:space="preserve" labels="VARIABLE">a</id>
                                      <apply>
                                        <pow />
                                        <id xml:space="preserve" labels="VARIABLE">t</id>
                                        <real>2</real>
                                      </apply>
                                    </apply>
                                    <apply>
                                      <mult />
                                      <id xml:space="preserve" labels="VARIABLE">b</id>
                                      <id xml:space="preserve" labels="VARIABLE">t</id>
                                    </apply>
                                  </apply>
                                </apply>
                              </apply>
                              <apply>
                                <plus />
                                <apply>
                                  <mult />
                                  <apply>
                                    <mult />
                                    <real>2</real>
                                    <id xml:space="preserve" labels="VARIABLE">a</id>
                                  </apply>
                                  <id xml:space="preserve" labels="VARIABLE">t</id>
                                </apply>
                                <id xml:space="preserve" labels="VARIABLE">b</id>
                              </apply>
                            </apply>
                          </apply>
                        </apply>
                      </parens>
                    </apply>
                    <apply>
                      <mult />
                      <real>8</real>
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="VARIABLE">a</id>
                        <apply>
                          <div />
                          <real>3</real>
                          <real>2</real>
                        </apply>
                      </apply>
                    </apply>
                  </apply>
                  <apply>
                    <plus />
                    <apply>
                      <div />
                      <apply>
                        <mult />
                        <parens>
                          <apply>
                            <plus />
                            <apply>
                              <mult />
                              <apply>
                                <mult />
                                <real>2</real>
                                <id xml:space="preserve" labels="VARIABLE">a</id>
                              </apply>
                              <id xml:space="preserve" labels="VARIABLE">t</id>
                            </apply>
                            <id xml:space="preserve" labels="VARIABLE">b</id>
                          </apply>
                        </parens>
                        <apply>
                          <nthRoot />
                          <placeholder />
                          <apply>
                            <plus />
                            <apply>
                              <mult />
                              <id xml:space="preserve" labels="VARIABLE">a</id>
                              <apply>
                                <pow />
                                <id xml:space="preserve" labels="VARIABLE">t</id>
                                <real>2</real>
                              </apply>
                            </apply>
                            <apply>
                              <mult />
                              <id xml:space="preserve" labels="VARIABLE">b</id>
                              <id xml:space="preserve" labels="VARIABLE">t</id>
                            </apply>
                          </apply>
                        </apply>
                      </apply>
                      <apply>
                        <mult />
                        <real>4</real>
                        <id xml:space="preserve" labels="VARIABLE">a</id>
                      </apply>
                    </apply>
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">c</id>
                      <id xml:space="preserve" labels="VARIABLE">t</id>
                    </apply>
                  </apply>
                </apply>
              </program>
            </then>
            <elseif>
              <test>
                <apply>
                  <and />
                  <apply>
                    <equal />
                    <id xml:space="preserve" labels="VARIABLE">a</id>
                    <real>0</real>
                  </apply>
                  <apply>
                    <notEqual />
                    <id xml:space="preserve" labels="VARIABLE">b</id>
                    <real>0</real>
                  </apply>
                </apply>
              </test>
              <then>
                <program>
                  <apply>
                    <div />
                    <apply>
                      <plus />
                      <apply>
                        <mult />
                        <real>3</real>
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">c</id>
                          <id xml:space="preserve" labels="VARIABLE">t</id>
                        </apply>
                      </apply>
                      <apply>
                        <mult />
                        <apply>
                          <mult />
                          <real>2</real>
                          <id xml:space="preserve" labels="VARIABLE">t</id>
                        </apply>
                        <apply>
                          <nthRoot />
                          <placeholder />
                          <apply>
                            <mult />
                            <id xml:space="preserve" labels="VARIABLE">b</id>
                            <id xml:space="preserve" labels="VARIABLE">t</id>
                          </apply>
                        </apply>
                      </apply>
                    </apply>
                    <real>3</real>
                  </apply>
                </program>
              </then>
            </elseif>
            <elseif>
              <test>
                <apply>
                  <and />
                  <apply>
                    <equal />
                    <id xml:space="preserve" labels="VARIABLE">a</id>
                    <real>0</real>
                  </apply>
                  <apply>
                    <equal />
                    <id xml:space="preserve" labels="VARIABLE">b</id>
                    <real>0</real>
                  </apply>
                </apply>
              </test>
              <then>
                <program>
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">c</id>
                    <id xml:space="preserve" labels="VARIABLE">t</id>
                  </apply>
                </program>
              </then>
            </elseif>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

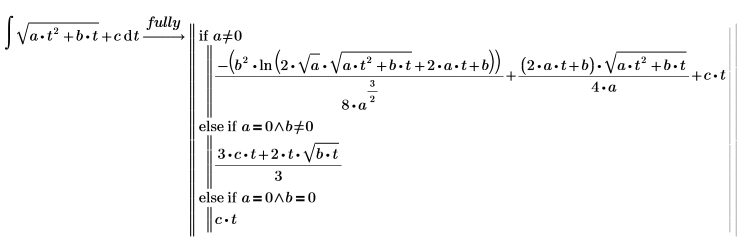
3. Evaluate the solution only for the cases when a≠0.

<region id="ID0EW1PMB" width="799.06066791852311" actualWidth="799.06066791852311" actualHeight="78.99026652623813" top="441.60000000000008" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="15">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t</id>
          </boundVars>
          <apply>
            <plus />
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <plus />
                <apply>
                  <mult />
                  <id xml:space="preserve">a</id>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                    <real>2</real>
                  </apply>
                </apply>
                <apply>
                  <mult />
                  <id xml:space="preserve">b</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                </apply>
              </apply>
            </apply>
            <id xml:space="preserve">c</id>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">fully</id>
            <id xml:space="preserve">assume</id>
          </sequence>
          <apply>
            <notEqual />
            <id xml:space="preserve">a</id>
            <real>0</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <plus />
            <apply>
              <div />
              <apply>
                <neg />
                <parens>
                  <apply>
                    <mult />
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">b</id>
                      <real>2</real>
                    </apply>
                    <apply>
                      <id xml:space="preserve" labels="FUNCTION">ln</id>
                      <apply>
                        <plus />
                        <apply>
                          <mult />
                          <apply>
                            <mult />
                            <real>2</real>
                            <apply>
                              <nthRoot />
                              <placeholder />
                              <id xml:space="preserve" labels="VARIABLE">a</id>
                            </apply>
                          </apply>
                          <apply>
                            <nthRoot />
                            <placeholder />
                            <apply>
                              <plus />
                              <apply>
                                <mult />
                                <id xml:space="preserve" labels="VARIABLE">a</id>
                                <apply>
                                  <pow />
                                  <id xml:space="preserve" labels="VARIABLE">t</id>
                                  <real>2</real>
                                </apply>
                              </apply>
                              <apply>
                                <mult />
                                <id xml:space="preserve" labels="VARIABLE">b</id>
                                <id xml:space="preserve" labels="VARIABLE">t</id>
                              </apply>
                            </apply>
                          </apply>
                        </apply>
                        <apply>
                          <plus />
                          <apply>
                            <mult />
                            <apply>
                              <mult />
                              <real>2</real>
                              <id xml:space="preserve" labels="VARIABLE">a</id>
                            </apply>
                            <id xml:space="preserve" labels="VARIABLE">t</id>
                          </apply>
                          <id xml:space="preserve" labels="VARIABLE">b</id>
                        </apply>
                      </apply>
                    </apply>
                  </apply>
                </parens>
              </apply>
              <apply>
                <mult />
                <real>8</real>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE">a</id>
                  <apply>
                    <div />
                    <real>3</real>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
            </apply>
            <apply>
              <div />
              <apply>
                <mult />
                <parens>
                  <apply>
                    <plus />
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <real>2</real>
                        <id xml:space="preserve" labels="VARIABLE">a</id>
                      </apply>
                      <id xml:space="preserve" labels="VARIABLE">t</id>
                    </apply>
                    <id xml:space="preserve" labels="VARIABLE">b</id>
                  </apply>
                </parens>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <plus />
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">a</id>
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="VARIABLE">t</id>
                        <real>2</real>
                      </apply>
                    </apply>
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">b</id>
                      <id xml:space="preserve" labels="VARIABLE">t</id>
                    </apply>
                  </apply>
                </apply>
              </apply>
              <apply>
                <mult />
                <real>4</real>
                <id xml:space="preserve" labels="VARIABLE">a</id>
              </apply>
            </apply>
          </apply>
          <apply>
            <mult />
            <id xml:space="preserve" labels="VARIABLE">c</id>
            <id xml:space="preserve" labels="VARIABLE">t</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

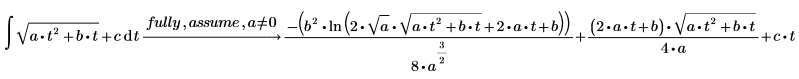
Linear Power Function

1. Evaluate a symbolic integral of a linear power function.

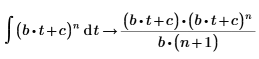
2. Evaluate the full conditioned solution of the integral, using the keyword fully.

<region id="ID0EH5PMB" actualWidth="275.24333333333334" actualHeight="160.86" top="633.60000000000014" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="17">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t</id>
          </boundVars>
          <apply>
            <pow />
            <parens>
              <apply>
                <plus />
                <apply>
                  <mult />
                  <id xml:space="preserve">b</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                </apply>
                <id xml:space="preserve">c</id>
              </apply>
            </parens>
            <id xml:space="preserve">n</id>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <id xml:space="preserve">fully</id>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <notEqual />
                <id xml:space="preserve" labels="VARIABLE">n</id>
                <real>-1</real>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <div />
                  <apply>
                    <pow />
                    <parens>
                      <apply>
                        <plus />
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">b</id>
                          <id xml:space="preserve" labels="VARIABLE">t</id>
                        </apply>
                        <id xml:space="preserve" labels="VARIABLE">c</id>
                      </apply>
                    </parens>
                    <apply>
                      <plus />
                      <id xml:space="preserve" labels="VARIABLE">n</id>
                      <real>1</real>
                    </apply>
                  </apply>
                  <apply>
                    <plus />
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">b</id>
                      <id xml:space="preserve" labels="VARIABLE">n</id>
                    </apply>
                    <id xml:space="preserve" labels="VARIABLE">b</id>
                  </apply>
                </apply>
              </program>
            </then>
            <elseif>
              <test>
                <apply>
                  <equal />
                  <id xml:space="preserve" labels="VARIABLE">n</id>
                  <real>-1</real>
                </apply>
              </test>
              <then>
                <program>
                  <apply>
                    <div />
                    <apply>
                      <id xml:space="preserve" labels="FUNCTION">ln</id>
                      <apply>
                        <plus />
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">b</id>
                          <id xml:space="preserve" labels="VARIABLE">t</id>
                        </apply>
                        <id xml:space="preserve" labels="VARIABLE">c</id>
                      </apply>
                    </apply>
                    <id xml:space="preserve" labels="VARIABLE">b</id>
                  </apply>
                </program>
              </then>
            </elseif>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

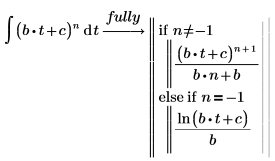
Elliptic Integral Functions

The complete elliptic integral function of the first kind:

1. Evaluate a symbolic integral of the complete elliptic integral function of the first kind.

<region id="ID0EIAQMB" width="683.62666666666678" actualWidth="683.62666666666678" actualHeight="57.800000000000004" top="825.60000000000014" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="18">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t</id>
          </boundVars>
          <apply>
            <mult />
            <id xml:space="preserve">A</id>
            <apply>
              <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">ellipticK</id>
              <apply>
                <plus />
                <apply>
                  <mult />
                  <id xml:space="preserve">c</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                </apply>
                <id xml:space="preserve">d</id>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <plus />
            <apply>
              <mult />
              <apply>
                <mult />
                <real>2</real>
                <id xml:space="preserve" labels="VARIABLE">A</id>
              </apply>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">c</id>
                    <id xml:space="preserve" labels="VARIABLE">t</id>
                  </apply>
                  <id xml:space="preserve" labels="VARIABLE">d</id>
                </apply>
              </apply>
            </apply>
            <apply>
              <mult />
              <parens>
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <real>2</real>
                        <id xml:space="preserve" labels="VARIABLE">A</id>
                      </apply>
                      <id xml:space="preserve" labels="VARIABLE">c</id>
                    </apply>
                    <id xml:space="preserve" labels="VARIABLE">t</id>
                  </apply>
                  <parens>
                    <apply>
                      <minus />
                      <apply>
                        <mult />
                        <apply>
                          <mult />
                          <real>2</real>
                          <id xml:space="preserve" labels="VARIABLE">A</id>
                        </apply>
                        <id xml:space="preserve" labels="VARIABLE">d</id>
                      </apply>
                      <apply>
                        <mult />
                        <real>2</real>
                        <id xml:space="preserve" labels="VARIABLE">A</id>
                      </apply>
                    </apply>
                  </parens>
                </apply>
              </parens>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ellipticK</id>
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">c</id>
                    <id xml:space="preserve" labels="VARIABLE">t</id>
                  </apply>
                  <id xml:space="preserve" labels="VARIABLE">d</id>
                </apply>
              </apply>
            </apply>
          </apply>
          <id xml:space="preserve" labels="VARIABLE">c</id>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

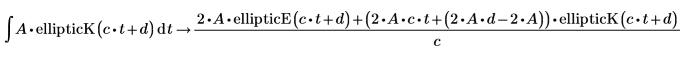
2. Evaluate the full conditioned solution of the complete elliptic integral function of the first kind, using the keyword fully.

<region id="ID0E3BQMB" width="750.59666666666669" actualWidth="750.59666666666669" actualHeight="136.10000000000002" top="921.60000000000014" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="19">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t</id>
          </boundVars>
          <apply>
            <mult />
            <id xml:space="preserve">A</id>
            <apply>
              <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">ellipticK</id>
              <apply>
                <plus />
                <apply>
                  <mult />
                  <id xml:space="preserve">c</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                </apply>
                <id xml:space="preserve">d</id>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <id xml:space="preserve">fully</id>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <notEqual />
                <id xml:space="preserve" labels="VARIABLE">c</id>
                <real>0</real>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <div />
                  <apply>
                    <plus />
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <real>2</real>
                        <id xml:space="preserve" labels="VARIABLE">A</id>
                      </apply>
                      <apply>
                        <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
                        <apply>
                          <plus />
                          <apply>
                            <mult />
                            <id xml:space="preserve" labels="VARIABLE">c</id>
                            <id xml:space="preserve" labels="VARIABLE">t</id>
                          </apply>
                          <id xml:space="preserve" labels="VARIABLE">d</id>
                        </apply>
                      </apply>
                    </apply>
                    <apply>
                      <mult />
                      <parens>
                        <apply>
                          <plus />
                          <apply>
                            <mult />
                            <apply>
                              <mult />
                              <apply>
                                <mult />
                                <real>2</real>
                                <id xml:space="preserve" labels="VARIABLE">A</id>
                              </apply>
                              <id xml:space="preserve" labels="VARIABLE">c</id>
                            </apply>
                            <id xml:space="preserve" labels="VARIABLE">t</id>
                          </apply>
                          <parens>
                            <apply>
                              <minus />
                              <apply>
                                <mult />
                                <apply>
                                  <mult />
                                  <real>2</real>
                                  <id xml:space="preserve" labels="VARIABLE">A</id>
                                </apply>
                                <id xml:space="preserve" labels="VARIABLE">d</id>
                              </apply>
                              <apply>
                                <mult />
                                <real>2</real>
                                <id xml:space="preserve" labels="VARIABLE">A</id>
                              </apply>
                            </apply>
                          </parens>
                        </apply>
                      </parens>
                      <apply>
                        <id xml:space="preserve" labels="FUNCTION">ellipticK</id>
                        <apply>
                          <plus />
                          <apply>
                            <mult />
                            <id xml:space="preserve" labels="VARIABLE">c</id>
                            <id xml:space="preserve" labels="VARIABLE">t</id>
                          </apply>
                          <id xml:space="preserve" labels="VARIABLE">d</id>
                        </apply>
                      </apply>
                    </apply>
                  </apply>
                  <id xml:space="preserve" labels="VARIABLE">c</id>
                </apply>
              </program>
            </then>
            <elseif>
              <test>
                <apply>
                  <equal />
                  <id xml:space="preserve" labels="VARIABLE">c</id>
                  <real>0</real>
                </apply>
              </test>
              <then>
                <program>
                  <apply>
                    <mult />
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">A</id>
                      <id xml:space="preserve" labels="VARIABLE">t</id>
                    </apply>
                    <apply>
                      <id xml:space="preserve" labels="FUNCTION">ellipticK</id>
                      <id xml:space="preserve" labels="VARIABLE">d</id>
                    </apply>
                  </apply>
                </program>
              </then>
            </elseif>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

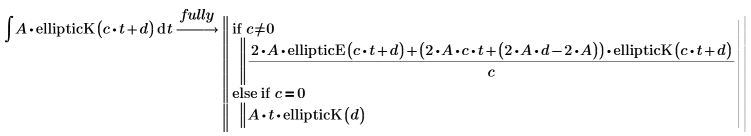
The incomplete elliptic integral function of the first kind:

1. Evaluate a symbolic integral of the incomplete elliptic integral function of the first kind.

<region id="ID0EUDQMB" actualWidth="712.204667605559" actualHeight="105.68860058197976" top="1094.4" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="20">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t</id>
          </boundVars>
          <apply>
            <mult />
            <apply>
              <mult />
              <id xml:space="preserve">A</id>
              <parens>
                <apply>
                  <mult />
                  <id xml:space="preserve">c</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                </apply>
              </parens>
            </apply>
            <apply>
              <div />
              <apply>
                <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">ellipticF</id>
                <sequence>
                  <apply>
                    <mult />
                    <id xml:space="preserve">c</id>
                    <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                  </apply>
                  <id xml:space="preserve">a</id>
                </sequence>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <minus />
                  <real>1</real>
                  <apply>
                    <pow />
                    <parens>
                      <apply>
                        <mult />
                        <id xml:space="preserve">c</id>
                        <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                      </apply>
                    </parens>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <minus />
            <apply>
              <mult />
              <id xml:space="preserve" labels="VARIABLE">A</id>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">atan</id>
                <apply>
                  <div />
                  <apply>
                    <mult />
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">c</id>
                      <id xml:space="preserve" labels="VARIABLE">t</id>
                    </apply>
                    <apply>
                      <nthRoot />
                      <placeholder />
                      <id xml:space="preserve" labels="VARIABLE">a</id>
                    </apply>
                  </apply>
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <apply>
                      <plus />
                      <apply>
                        <neg />
                        <parens>
                          <apply>
                            <mult />
                            <apply>
                              <mult />
                              <id xml:space="preserve" labels="VARIABLE">a</id>
                              <apply>
                                <pow />
                                <id xml:space="preserve" labels="VARIABLE">c</id>
                                <real>2</real>
                              </apply>
                            </apply>
                            <apply>
                              <pow />
                              <id xml:space="preserve" labels="VARIABLE">t</id>
                              <real>2</real>
                            </apply>
                          </apply>
                        </parens>
                      </apply>
                      <real>1</real>
                    </apply>
                  </apply>
                </apply>
              </apply>
            </apply>
            <apply>
              <mult />
              <apply>
                <mult />
                <apply>
                  <mult />
                  <id xml:space="preserve" labels="VARIABLE">A</id>
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <apply>
                      <plus />
                      <apply>
                        <neg />
                        <parens>
                          <apply>
                            <mult />
                            <apply>
                              <pow />
                              <id xml:space="preserve" labels="VARIABLE">c</id>
                              <real>2</real>
                            </apply>
                            <apply>
                              <pow />
                              <id xml:space="preserve" labels="VARIABLE">t</id>
                              <real>2</real>
                            </apply>
                          </apply>
                        </parens>
                      </apply>
                      <real>1</real>
                    </apply>
                  </apply>
                </apply>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <id xml:space="preserve" labels="VARIABLE">a</id>
                </apply>
              </apply>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
                <sequence>
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">c</id>
                    <id xml:space="preserve" labels="VARIABLE">t</id>
                  </apply>
                  <id xml:space="preserve" labels="VARIABLE">a</id>
                </sequence>
              </apply>
            </apply>
          </apply>
          <apply>
            <mult />
            <id xml:space="preserve" labels="VARIABLE">c</id>
            <apply>
              <nthRoot />
              <placeholder />
              <id xml:space="preserve" labels="VARIABLE">a</id>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

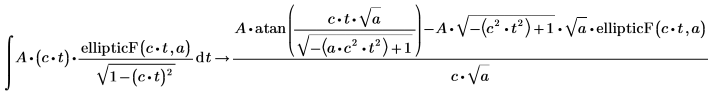
2. Evaluate the full conditioned solution of the incomplete elliptic integral function of the first kind, using the keyword fully.

<region id="ID0EIFQMB" width="779.17466760555908" actualWidth="779.17466760555908" actualHeight="259.48986744263965" top="1190.4" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="21">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t</id>
          </boundVars>
          <apply>
            <mult />
            <apply>
              <mult />
              <id xml:space="preserve">A</id>
              <parens>
                <apply>
                  <mult />
                  <id xml:space="preserve">c</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                </apply>
              </parens>
            </apply>
            <apply>
              <div />
              <apply>
                <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">ellipticF</id>
                <sequence>
                  <apply>
                    <mult />
                    <id xml:space="preserve">c</id>
                    <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                  </apply>
                  <id xml:space="preserve">a</id>
                </sequence>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <minus />
                  <real>1</real>
                  <apply>
                    <pow />
                    <parens>
                      <apply>
                        <mult />
                        <id xml:space="preserve">c</id>
                        <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                      </apply>
                    </parens>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <id xml:space="preserve">fully</id>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <and />
                <apply>
                  <notEqual />
                  <id xml:space="preserve" labels="VARIABLE">c</id>
                  <real>0</real>
                </apply>
                <apply>
                  <notEqual />
                  <id xml:space="preserve" labels="VARIABLE">a</id>
                  <real>0</real>
                </apply>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <div />
                  <apply>
                    <minus />
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">A</id>
                      <apply>
                        <id xml:space="preserve" labels="FUNCTION">atan</id>
                        <apply>
                          <div />
                          <apply>
                            <mult />
                            <apply>
                              <mult />
                              <id xml:space="preserve" labels="VARIABLE">c</id>
                              <id xml:space="preserve" labels="VARIABLE">t</id>
                            </apply>
                            <apply>
                              <nthRoot />
                              <placeholder />
                              <id xml:space="preserve" labels="VARIABLE">a</id>
                            </apply>
                          </apply>
                          <apply>
                            <nthRoot />
                            <placeholder />
                            <apply>
                              <plus />
                              <apply>
                                <neg />
                                <parens>
                                  <apply>
                                    <mult />
                                    <apply>
                                      <mult />
                                      <id xml:space="preserve" labels="VARIABLE">a</id>
                                      <apply>
                                        <pow />
                                        <id xml:space="preserve" labels="VARIABLE">c</id>
                                        <real>2</real>
                                      </apply>
                                    </apply>
                                    <apply>
                                      <pow />
                                      <id xml:space="preserve" labels="VARIABLE">t</id>
                                      <real>2</real>
                                    </apply>
                                  </apply>
                                </parens>
                              </apply>
                              <real>1</real>
                            </apply>
                          </apply>
                        </apply>
                      </apply>
                    </apply>
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">A</id>
                          <apply>
                            <nthRoot />
                            <placeholder />
                            <apply>
                              <plus />
                              <apply>
                                <neg />
                                <parens>
                                  <apply>
                                    <mult />
                                    <apply>
                                      <pow />
                                      <id xml:space="preserve" labels="VARIABLE">c</id>
                                      <real>2</real>
                                    </apply>
                                    <apply>
                                      <pow />
                                      <id xml:space="preserve" labels="VARIABLE">t</id>
                                      <real>2</real>
                                    </apply>
                                  </apply>
                                </parens>
                              </apply>
                              <real>1</real>
                            </apply>
                          </apply>
                        </apply>
                        <apply>
                          <nthRoot />
                          <placeholder />
                          <id xml:space="preserve" labels="VARIABLE">a</id>
                        </apply>
                      </apply>
                      <apply>
                        <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
                        <sequence>
                          <apply>
                            <mult />
                            <id xml:space="preserve" labels="VARIABLE">c</id>
                            <id xml:space="preserve" labels="VARIABLE">t</id>
                          </apply>
                          <id xml:space="preserve" labels="VARIABLE">a</id>
                        </sequence>
                      </apply>
                    </apply>
                  </apply>
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">c</id>
                    <apply>
                      <nthRoot />
                      <placeholder />
                      <id xml:space="preserve" labels="VARIABLE">a</id>
                    </apply>
                  </apply>
                </apply>
              </program>
            </then>
            <elseif>
              <test>
                <apply>
                  <and />
                  <apply>
                    <notEqual />
                    <id xml:space="preserve" labels="VARIABLE">c</id>
                    <real>0</real>
                  </apply>
                  <apply>
                    <equal />
                    <id xml:space="preserve" labels="VARIABLE">a</id>
                    <real>0</real>
                  </apply>
                </apply>
              </test>
              <then>
                <program>
                  <apply>
                    <div />
                    <apply>
                      <plus />
                      <apply>
                        <neg />
                        <parens>
                          <apply>
                            <mult />
                            <apply>
                              <mult />
                              <id xml:space="preserve" labels="VARIABLE">A</id>
                              <apply>
                                <nthRoot />
                                <placeholder />
                                <apply>
                                  <plus />
                                  <apply>
                                    <neg />
                                    <parens>
                                      <apply>
                                        <mult />
                                        <apply>
                                          <pow />
                                          <id xml:space="preserve" labels="VARIABLE">c</id>
                                          <real>2</real>
                                        </apply>
                                        <apply>
                                          <pow />
                                          <id xml:space="preserve" labels="VARIABLE">t</id>
                                          <real>2</real>
                                        </apply>
                                      </apply>
                                    </parens>
                                  </apply>
                                  <real>1</real>
                                </apply>
                              </apply>
                            </apply>
                            <apply>
                              <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
                              <sequence>
                                <apply>
                                  <mult />
                                  <id xml:space="preserve" labels="VARIABLE">c</id>
                                  <id xml:space="preserve" labels="VARIABLE">t</id>
                                </apply>
                                <real>0</real>
                              </sequence>
                            </apply>
                          </apply>
                        </parens>
                      </apply>
                      <apply>
                        <mult />
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">A</id>
                          <id xml:space="preserve" labels="VARIABLE">c</id>
                        </apply>
                        <id xml:space="preserve" labels="VARIABLE">t</id>
                      </apply>
                    </apply>
                    <id xml:space="preserve" labels="VARIABLE">c</id>
                  </apply>
                </program>
              </then>
            </elseif>
            <elseif>
              <test>
                <apply>
                  <equal />
                  <id xml:space="preserve" labels="VARIABLE">c</id>
                  <real>0</real>
                </apply>
              </test>
              <then>
                <program>
                  <real>0</real>
                </program>
              </then>
            </elseif>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Trigonometric Functions

The cos function:

1. Evaluate a symbolic integral of the cos function.

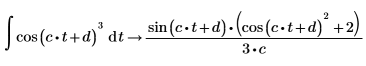
2. Evaluate the full conditioned solution of the cos function, using the keyword fully.

<region id="ID0EKJQMB" actualWidth="432.89333333333343" actualHeight="161.3" top="1555.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="23">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t</id>
          </boundVars>
          <apply>
            <pow />
            <apply>
              <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">cos</id>
              <apply>
                <plus />
                <apply>
                  <mult />
                  <id xml:space="preserve">c</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t</id>
                </apply>
                <id xml:space="preserve">d</id>
              </apply>
            </apply>
            <real>3</real>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <id xml:space="preserve">fully</id>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <notEqual />
                <id xml:space="preserve" labels="VARIABLE">c</id>
                <real>0</real>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <div />
                  <apply>
                    <mult />
                    <apply>
                      <id xml:space="preserve" labels="FUNCTION">sin</id>
                      <apply>
                        <plus />
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">c</id>
                          <id xml:space="preserve" labels="VARIABLE">t</id>
                        </apply>
                        <id xml:space="preserve" labels="VARIABLE">d</id>
                      </apply>
                    </apply>
                    <parens>
                      <apply>
                        <plus />
                        <apply>
                          <pow />
                          <apply>
                            <id xml:space="preserve" labels="FUNCTION">cos</id>
                            <apply>
                              <plus />
                              <apply>
                                <mult />
                                <id xml:space="preserve" labels="VARIABLE">c</id>
                                <id xml:space="preserve" labels="VARIABLE">t</id>
                              </apply>
                              <id xml:space="preserve" labels="VARIABLE">d</id>
                            </apply>
                          </apply>
                          <real>2</real>
                        </apply>
                        <real>2</real>
                      </apply>
                    </parens>
                  </apply>
                  <apply>
                    <mult />
                    <real>3</real>
                    <id xml:space="preserve" labels="VARIABLE">c</id>
                  </apply>
                </apply>
              </program>
            </then>
            <elseif>
              <test>
                <apply>
                  <equal />
                  <id xml:space="preserve" labels="VARIABLE">c</id>
                  <real>0</real>
                </apply>
              </test>
              <then>
                <program>
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">t</id>
                    <apply>
                      <pow />
                      <apply>
                        <id xml:space="preserve" labels="FUNCTION">cos</id>
                        <id xml:space="preserve" labels="VARIABLE">d</id>
                      </apply>
                      <real>3</real>
                    </apply>
                  </apply>
                </program>
              </then>
            </elseif>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

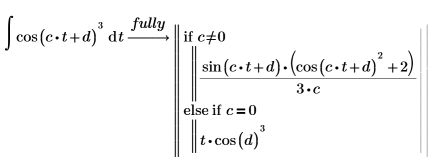
The sin function:

1. Evaluate a symbolic integral of the sin function.

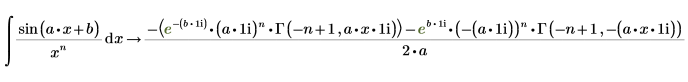
2. Evaluate the full conditioned solution of the sin function, using the keyword fully.

<region id="ID0EDNQMB" width="755.41666666666663" actualWidth="755.41666666666663" actualHeight="173.79733333333334" top="1920.0000000000005" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="25">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">x</id>
          </boundVars>
          <apply>
            <div />
            <apply>
              <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">sin</id>
              <apply>
                <plus />
                <apply>
                  <mult />
                  <id xml:space="preserve">a</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
                </apply>
                <id xml:space="preserve">b</id>
              </apply>
            </apply>
            <apply>
              <pow />
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
              <id xml:space="preserve">n</id>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <id xml:space="preserve">fully</id>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <notEqual />
                <id xml:space="preserve" labels="VARIABLE">a</id>
                <real>0</real>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <div />
                  <apply>
                    <minus />
                    <apply>
                      <neg />
                      <parens>
                        <apply>
                          <mult />
                          <apply>
                            <mult />
                            <apply>
                              <pow />
                              <id xml:space="preserve" labels="CONSTANT">e</id>
                              <apply>
                                <neg />
                                <parens>
                                  <apply>
                                    <mult />
                                    <id xml:space="preserve" labels="VARIABLE">b</id>
                                    <imag symbol="i">1</imag>
                                  </apply>
                                </parens>
                              </apply>
                            </apply>
                            <apply>
                              <pow />
                              <parens>
                                <apply>
                                  <mult />
                                  <id xml:space="preserve" labels="VARIABLE">a</id>
                                  <imag symbol="i">1</imag>
                                </apply>
                              </parens>
                              <id xml:space="preserve" labels="VARIABLE">n</id>
                            </apply>
                          </apply>
                          <apply>
                            <id xml:space="preserve" labels="FUNCTION">Γ</id>
                            <sequence>
                              <apply>
                                <plus />
                                <apply>
                                  <neg />
                                  <id xml:space="preserve" labels="VARIABLE">n</id>
                                </apply>
                                <real>1</real>
                              </apply>
                              <apply>
                                <mult />
                                <apply>
                                  <mult />
                                  <id xml:space="preserve" labels="VARIABLE">a</id>
                                  <id xml:space="preserve" labels="VARIABLE">x</id>
                                </apply>
                                <imag symbol="i">1</imag>
                              </apply>
                            </sequence>
                          </apply>
                        </apply>
                      </parens>
                    </apply>
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <apply>
                          <pow />
                          <id xml:space="preserve" labels="CONSTANT">e</id>
                          <apply>
                            <mult />
                            <id xml:space="preserve" labels="VARIABLE">b</id>
                            <imag symbol="i">1</imag>
                          </apply>
                        </apply>
                        <apply>
                          <pow />
                          <parens>
                            <apply>
                              <neg />
                              <parens>
                                <apply>
                                  <mult />
                                  <id xml:space="preserve" labels="VARIABLE">a</id>
                                  <imag symbol="i">1</imag>
                                </apply>
                              </parens>
                            </apply>
                          </parens>
                          <id xml:space="preserve" labels="VARIABLE">n</id>
                        </apply>
                      </apply>
                      <apply>
                        <id xml:space="preserve" labels="FUNCTION">Γ</id>
                        <sequence>
                          <apply>
                            <plus />
                            <apply>
                              <neg />
                              <id xml:space="preserve" labels="VARIABLE">n</id>
                            </apply>
                            <real>1</real>
                          </apply>
                          <apply>
                            <neg />
                            <parens>
                              <apply>
                                <mult />
                                <apply>
                                  <mult />
                                  <id xml:space="preserve" labels="VARIABLE">a</id>
                                  <id xml:space="preserve" labels="VARIABLE">x</id>
                                </apply>
                                <imag symbol="i">1</imag>
                              </apply>
                            </parens>
                          </apply>
                        </sequence>
                      </apply>
                    </apply>
                  </apply>
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="VARIABLE">a</id>
                  </apply>
                </apply>
              </program>
            </then>
            <elseif>
              <test>
                <apply>
                  <equal />
                  <id xml:space="preserve" labels="VARIABLE">a</id>
                  <real>0</real>
                </apply>
              </test>
              <then>
                <program>
                  <apply>
                    <div />
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">x</id>
                          <imag symbol="i">1</imag>
                        </apply>
                        <parens>
                          <apply>
                            <minus />
                            <apply>
                              <pow />
                              <id xml:space="preserve" labels="CONSTANT">e</id>
                              <apply>
                                <mult />
                                <apply>
                                  <mult />
                                  <real>2</real>
                                  <id xml:space="preserve" labels="VARIABLE">b</id>
                                </apply>
                                <imag symbol="i">1</imag>
                              </apply>
                            </apply>
                            <real>1</real>
                          </apply>
                        </parens>
                      </apply>
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="CONSTANT">e</id>
                        <apply>
                          <neg />
                          <parens>
                            <apply>
                              <mult />
                              <id xml:space="preserve" labels="VARIABLE">b</id>
                              <imag symbol="i">1</imag>
                            </apply>
                          </parens>
                        </apply>
                      </apply>
                    </apply>
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <real>2</real>
                        <parens>
                          <apply>
                            <minus />
                            <id xml:space="preserve" labels="VARIABLE">n</id>
                            <real>1</real>
                          </apply>
                        </parens>
                      </apply>
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="VARIABLE">x</id>
                        <id xml:space="preserve" labels="VARIABLE">n</id>
                      </apply>
                    </apply>
                  </apply>
                </program>
              </then>
            </elseif>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
    <formattingOverride BackgroundColor="#00FFFFFF" />
  </math>
</region>