Logarithmic Integral Functions
Logarithmic integral function li(x) is a special function for solving certain problems in physics and number theory. It provides a very good approximation to the prime counting function - that finds the number of prime numbers less than or equal to a given value.
• li(x)—Returns the logarithmic integral of x, which is defined for all positive real numbers, where x ≠ 1.
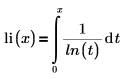
The integral for x>1 is interpreted as the Cauchy principal value.
The function 1/ln(x) has a singularity at x=1:
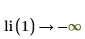
• The logarithmic integral function is related to the Exponential integral function as follows, for x>0:
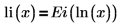
Li(x) — Returns the offset logarithmic integral function of x, which is defined as follows:
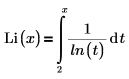
Arguments
• x is a real or complex scalar, or a vector of real or complex scalars.
Additional Information
• You can only evaluate the logarithmic integral function and the offset logarithmic integral function symbolically.