Gewöhnliche Differentialgleichungen lösen
Mithilfe von Lösungsblöcken und der Funktion odesolve können Sie eine Funktion finden, mit der eine gewöhnliche Differentialgleichung über einen bestimmten Wertebereich gelöst wird.
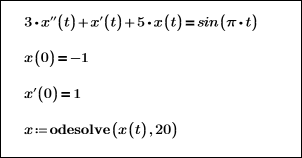
In diesem Fall wird die Ausgabefunktion über den folgenden Bereich 0 ≤ x ≤ 20 gelöst:
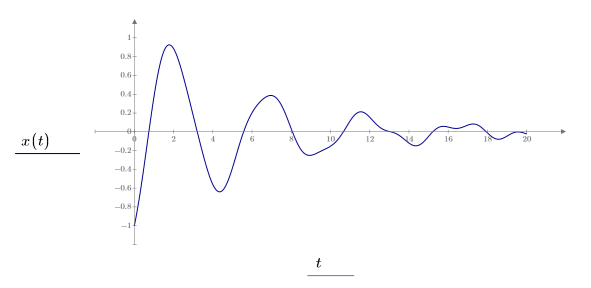
Bei Verwendung von GDGs in Lösungsblöcken gelten die folgenden Randbedingungen:
• Operatoren – Verwenden Sie den Gleichheitsoperator zum Lösen der GDGs. Verwenden Sie nicht die Vergleichsoperatoren oder den Ungleichheitsoperator. Verwenden Sie zum Definieren von Ableitungen den Operator für Ableitungen oder gewöhnliche Ableitungen, beispielsweise d/dx und d2/dx2 oder y'(x) und y''(x).
• Anfangs- oder Randbedingungen – Für eine einzelne gewöhnliche Differentialgleichung n-ter Ordnung muss es n unabhängige Gleichheitsbedingungen geben:
◦ Anfangswertproblem – Die Werte von y(x) und ihrer ersten n − 1-Ableitungen an einem einzelnen Startpunkt a werden benötigt.
◦ Randwertproblem – Die n Bedingungen müssen bestimmte Werte von y(x) und den zugehörigen Ableitungen am Anfangspunkt a oder am Endpunkt b angeben. Die Bedingungen müssen die Anforderungen für die Eingaben für die Funktion sbval erfüllen. Die Funktion odesolve ruft sbval auf, wenn Sie Randwertbedingungen angeben.
In jedem Fall müssen die in den Randbedingungen verwendeten Endpunkte mit den im Befehl odesolve angegebenen Endpunkten übereinstimmen. PTC Mathcad überprüft, ob Art und Anzahl der Bedingungen korrekt sind, und gibt bei einem Fehler eine entsprechende Meldung aus.
Die Leibnitz-Notation für die Ableitung dy/dx wird zum Festlegen der Anfangsbedingungen nicht unterstützt. Verwenden Sie stattdessen y’, den Operator für gewöhnliche Ableitungen, der als Lagrange-Notation bekannt ist. |
• Algebraische Bedingungen – Sie können algebraische Bedingungen wie y(b) + z(b) = w(b) hinzufügen. Der Lösungsblock enthält dann eine zusätzliche unbekannte Funktion w, die Sie als eine der Ausgabefunktionen in odesolve angeben müssen.
• Ausgabe – Sie müssen die Ausgabe der Funktion odesolve ohne Argumente entweder einem Funktionsnamen oder einem Vektor von Funktionsnamen zuweisen.
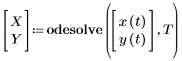
Das implizite Argument für diese Funktionen, ist die Integrationsvariable:

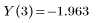
Lösungsmethoden
• Je nach Ausmaß des Problems und der verwendeten relativen Schrittweite müssen Sie eventuell den Wert von TOL verringern, um geeignete Lösungen zu erhalten. Versuchen Sie dies, wenn PTC Mathcad odesolve meldet, dass zu viele Integratorschritte vorhanden sind.
• Die Funktionen, die gelöst werden, dürfen im Integrationsintervall keine Singularitäten enthalten. Andernfalls produzieren sie unter Umständen unzuverlässige Ergebnisse.
• Beim Lösen von Problemen mit periodischem Verhalten über viele Zyklen kann ein Aliasing auftreten. Um in den Ergebnissen die erwarteten Frequenzen zu erhalten, erhöhen Sie die Anzahl der Interpolationspunkte.
• Um eine gewöhnliche Differentialgleichung zu lösen, die im höchsten Ableitungsausdruck nicht linear ist, oder um gewöhnliche Differentialgleichungen in einer Programmschleife zu lösen, verwenden Sie rkfixed oder einen anderen Befehlszeilen-GDG-Löser. Sie haben außerdem die Möglichkeit, die Ausgabe eines parametrisierten Lösungsblocks in einer Programmschleife mithilfe lokaler Funktionen zuzuweisen.