Nichtlineare Regression
genfit(vx, vy, vg, F)– Übergibt einen Vektor mit den Parametern, mit denen sich eine Funktion F von x und n Parametern u1... un am ehesten den Daten in vx und vy annähert.
Die Funktion genfit wendet eine optimierte Version des Levenberg-Marquardt-Verfahrens zur Minimierung an. Obwohl häufig schneller und weniger empfindlich gegenüber schlechten Schätzwerten, konvergiert diese Implementierung bei Problemen mit vielen lokalen Minima möglicherweise nicht gut, z.B. bei rationalen Funktionen. Diese Implementierung ist anfällig für fehlerhafte Ableitungsvektoren.
Argumente
• vx, vy sind Vektoren aus reellen Datenwerten derselben Länge, entsprechend den x- und y-Werten im Datensatz. Es müssen mindestens genauso viele Datenpunkte wie Parameter vorhanden sein.
• vg ist ein n Elementvektor von Schätzwerten für die Parameter. Wenn n = 1, dann ist vg ein Skalar.
• F(x, u) ist eine Anpassungsfunktion oder ein Vektor von Funktionen; dabei ist x die unabhängige Variable, und u ist entweder ein Vektor aus Parametern oder aus einzelnen Parameternamen. Die folgende Gleichung ist eine gültige Darstellung für eine Anpassungsfunktion:
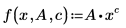
• n ist eine positive Ganzzahl. Die nicht vektorisierten Parameter sind auf neun unterschiedliche Namen begrenzt.
Konvergenz verbessern
Um die Konvergenz und eventuell die Genauigkeit von genfit zu verbessern, können Sie F als einen n+1-Vektor von Funktionen darstellen, in denen der erste Eintrag F0 die Anpassungsfunktion f ist und die restlichen Einträge F1 F2, …, Fn die symbolischen partiellen Ableitungen von f in Bezug auf die n Parameter sind.
Bei den beiden Arten der Darstellung der oben dargestellten Anpassungsfunktion können Sie f(x,A,c) nur verwenden, wenn Sie die partiellen Ableitungen symbolisch suchen. Wenn F als ein Vektor von Funktionen dargestellt wird, gilt daher für n ein Grenzwert von 9, sodass F eine maximale Länge von 10 hat. Sie können den Vektor F erstellen, indem Sie eine Matrix der entsprechenden partiellen Ableitungen erstellen und sie symbolisch auswerten:
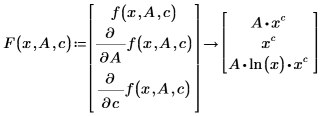
Zusätzliche Informationen
• Übergeben Sie an genfit nur den Namen der Anpassungsfunktion oder des Funktionsvektors ohne weitere Argumente.
• Wenn Sie die Anpassungsfunktion ohne die partiellen Ableitungen des symbolischen Parameters verwenden, berechnet genfit die partiellen Parameterableitungen numerisch. Dieses Verfahren ist zwar ungenauer als die Bereitstellung der symbolischen Ableitungen, kann in bestimmten Fällen jedoch von Vorteil sein.
• Wenn die Konvertierung mit genfit fehlschlägt, können Sie es mit der alternativen Levenberg-Marquardt-Methode oder anderen Schätzwerten versuchen oder Ihre Daten so skalieren, dass alle Parameter eine ähnliche Größenordnung haben.
• Der Lösungsalgorithmus Optimierter Levenberg-Marquardt reagiert empfindlicher auf Fehler in den bereitgestellten algebraischen Ableitungen. Wenn diese Methode fehlschlägt, überprüfen Sie die Ableitungsausdrücke.
• Wie bei allen numerischen Lösungsverfahren reagieren nichtlineare Probleme sehr stark auf Schätzwerte. Sie können die Anpassungsfunktion mit den Schätzwerten plotten, um die Schätzwerte zu optimieren, bevor Sie genfit verwenden.