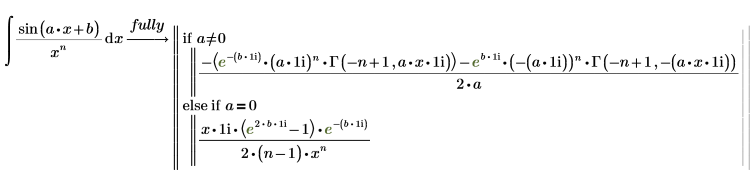Beispiel: Symbolische Integralfunktionen mit Schlüsselwort fully
Verwenden Sie das Schlüsselwort fully, um eine vollständige detaillierte Lösung für eine Symbolfunktion zu erhalten. Mithilfe von fully können Sie Lösungen für verschiedene Werte der Funktionskoeffizienten ermitteln. Im folgenden Beispiel: a, b und c. Verwenden Sie das Schlüsselwort assume, um die Lösung auf nur einen Wert der Funktionskoeffizienten einzuschränken.
1. Werten Sie ein symbolisches Integral aus.
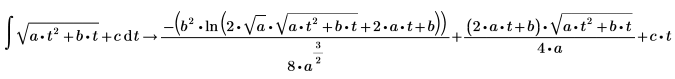
2. Werten Sie die vollständige bedingte Lösung des Integrals mit dem Schlüsselwort fully aus.
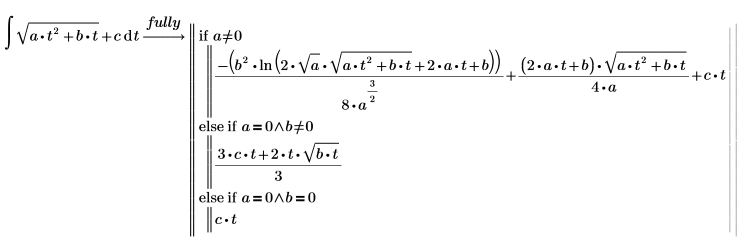
3. Werten Sie die Lösung nur für Fälle aus, in denen a≠0.
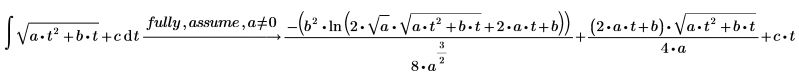
Lineare Potenzfunktion
1. Werten Sie ein symbolisches Integral einer linearen Potenzfunktion aus.
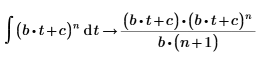
2. Werten Sie die vollständige bedingte Lösung des Integrals mit dem Schlüsselwort fully aus.
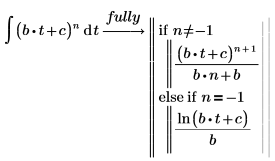
Elliptische Integralfunktionen
Vollständige elliptische Integralfunktion erster Art:
1. Werten Sie ein symbolisches Integral der vollständigen elliptischen Integralfunktion erster Art aus.
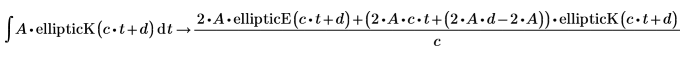
2. Werten Sie die vollständige bedingte Lösung der vollständigen elliptischen Integralfunktion erster Art mit dem Schlüsselwort fully aus.
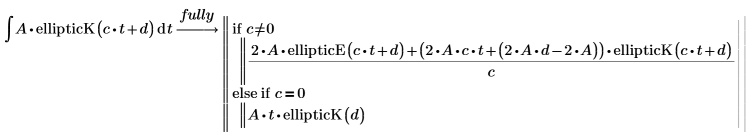
Unvollständige elliptische Integralfunktion erster Art:
1. Werten Sie ein symbolisches Integral der unvollständigen elliptischen Integralfunktion erster Art aus.
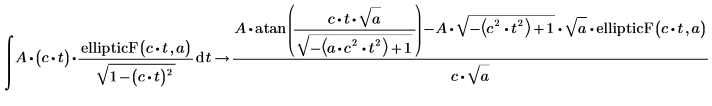
2. Werten Sie die vollständige bedingte Lösung der unvollständigen elliptischen Integralfunktion erster Art mit dem Schlüsselwort fully aus.

Trigonometrische Funktionen
Die Funktion cos:
1. Werten Sie ein symbolisches Integral der Funktion cos aus.
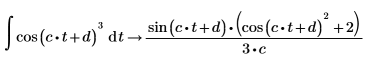
2. Werten Sie die vollständige bedingte Lösung der Funktion cos mit dem Schlüsselwort fully aus.
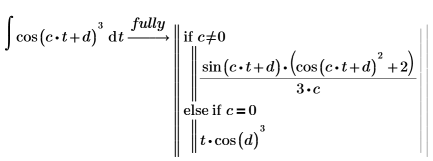
Die Funktion sin:
1. Werten Sie ein symbolisches Integral der Funktion sin aus.
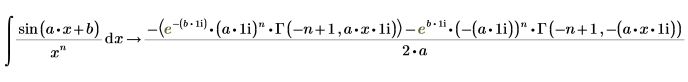
2. Werten Sie die vollständige bedingte Lösung der Funktion sin mit dem Schlüsselwort fully aus.