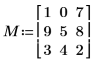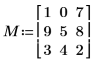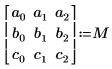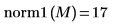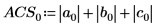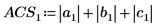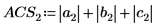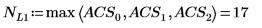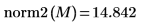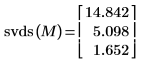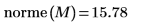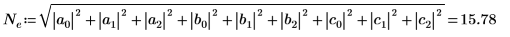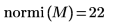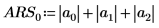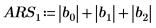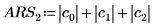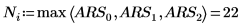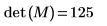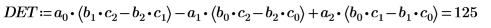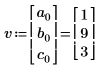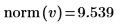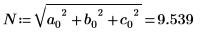Example: Matrix Norm and Determinant Functions

Functions > Vector and Matrix > Array Characteristics > Example: Matrix Norm and Determinant Functions

Example: Matrix Norm and Determinant Functions

1. Define a square matrix.

Click to copy this expression

2. Set the matrix elements to generic variable names.

Click to copy this expression

<region id="ID0ENVSDB" top="230.40000000000003" left="38.400000000000006" actualWidth="111.93333333333334" actualHeight="69.37360000000001" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="44">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <matrix rows="3" cols="3">
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
        </id>
      </matrix>
      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

3. Use the norm1 function to find the L1 norm of matrix M.

Click to copy this expression

Alternatively, find the L1 norm by calculating the maximum of the absolute column sums of M.

Click to copy this expression

<region id="ID0EJYSDB" top="403.20000000000005" left="38.400000000000006" actualWidth="156.98000000000002" actualHeight="27.791200000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="48">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
  </math>
</region>

Click to copy this expression

<region id="ID0EZYSDB" top="441.60000000000008" left="38.400000000000006" actualWidth="156.98000000000002" actualHeight="27.791200000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="50">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
  </math>
</region>

Click to copy this expression

<region id="ID0EJZSDB" top="480.00000000000006" left="38.400000000000006" actualWidth="156.98000000000002" actualHeight="27.791200000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="52">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
  </math>
</region>

Click to copy this expression

<region id="ID0EZZSDB" top="518.40000000000009" left="38.400000000000006" actualWidth="261.61666666666667" actualHeight="27.791200000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="54">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">N<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">L1</Subscript></Span>
      </id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">max</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

4. Use the norm2 function to find the L2 norm of matrix M.

Click to copy this expression

Alternatively, use the svds function to find the largest absolute singular value of matrix M.

Click to copy this expression

The svds function returns a vector of sorted singular values, so the top value is the largest singular value of matrix M.

5. Use the norme function to find the Euclidean norm of matrix M.

Click to copy this expression

Alternatively, manually calculate the square root of the sum of the absolute squares of matrix M.

Click to copy this expression

<region id="ID0EP6SDB" top="940.80000000000018" left="38.400000000000006" actualWidth="509.50600031296426" actualHeight="36.780453040075308" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="62">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">N<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">e</Subscript></Span>
      </id>
      <eval>
        <apply>
          <nthRoot />
          <placeholder />
          <apply>
            <plus />
            <apply>
              <plus />
              <apply>
                <plus />
                <apply>
                  <plus />
                  <apply>
                    <plus />
                    <apply>
                      <plus />
                      <apply>
                        <plus />
                        <apply>
                          <plus />
                          <apply>
                            <pow />
                            <apply>
                              <absval />
                              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                              </id>
                            </apply>
                            <real>2</real>
                          </apply>
                          <apply>
                            <pow />
                            <apply>
                              <absval />
                              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                              </id>
                            </apply>
                            <real>2</real>
                          </apply>
                        </apply>
                        <apply>
                          <pow />
                          <apply>
                            <absval />
                            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                            </id>
                          </apply>
                          <real>2</real>
                        </apply>
                      </apply>
                      <apply>
                        <pow />
                        <apply>
                          <absval />
                          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                          </id>
                        </apply>
                        <real>2</real>
                      </apply>
                    </apply>
                    <apply>
                      <pow />
                      <apply>
                        <absval />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                        </id>
                      </apply>
                      <real>2</real>
                    </apply>
                  </apply>
                  <apply>
                    <pow />
                    <apply>
                      <absval />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                      </id>
                    </apply>
                    <real>2</real>
                  </apply>
                </apply>
                <apply>
                  <pow />
                  <apply>
                    <absval />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                  </apply>
                  <real>2</real>
                </apply>
              </apply>
              <apply>
                <pow />
                <apply>
                  <absval />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                  </id>
                </apply>
                <real>2</real>
              </apply>
            </apply>
            <apply>
              <pow />
              <apply>
                <absval />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                </id>
              </apply>
              <real>2</real>
            </apply>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

6. Use the normi function to find the Infinity norm of matrix M.

Click to copy this expression

Alternatively, use the max function to manually calculate the maximum of the absolute row sums of matrix M.

Click to copy this expression

<region id="ID0E3BTDB" top="1132.8000000000002" left="38.400000000000006" actualWidth="158.77333333333334" actualHeight="27.791200000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="66">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Click to copy this expression

<region id="ID0EMCTDB" top="1171.2000000000003" left="38.400000000000006" actualWidth="156.48333333333335" actualHeight="27.791200000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="68">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Click to copy this expression

<region id="ID0E3CTDB" top="1209.6000000000001" left="38.400000000000006" actualWidth="155.11333333333334" actualHeight="27.791200000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="70">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Click to copy this expression

<region id="ID0EMDTDB" top="1248.0000000000002" left="38.400000000000006" actualWidth="252.23666666666671" actualHeight="27.791200000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="72">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">N<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">i</Subscript></Span>
      </id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">max</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

7. Use the det function to find the determinant of matrix M.

Click to copy this expression

Alternatively, manually calculate the determinant of matrix M.

Click to copy this expression

<region id="ID0EZFTDB" top="1401.6000000000001" left="38.400000000000006" actualWidth="490.83" actualHeight="27.791200000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="76">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">DET</id>
      <eval>
        <apply>
          <plus />
          <apply>
            <minus />
            <apply>
              <mult />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
              </id>
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                  </apply>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                    </id>
                  </apply>
                </apply>
              </parens>
            </apply>
            <apply>
              <mult />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
              </id>
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                  </apply>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                  </apply>
                </apply>
              </parens>
            </apply>
          </apply>
          <apply>
            <mult />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
            <parens>
              <apply>
                <minus />
                <apply>
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                  </id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                  </id>
                </apply>
                <apply>
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                  </id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                  </id>
                </apply>
              </apply>
            </parens>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

8. Use the norm function to find the norm of a vector containing the elements of column 0 of matrix M.

Click to copy this expression

<region id="ID0ESHTDB" top="1497.6000000000001" left="38.400000000000006" actualWidth="109.26666666666668" actualHeight="69.37360000000001" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="78">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">v</id>
      <eval>
        <matrix rows="3" cols="1">
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
        </matrix>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
  </math>
</region>

Click to copy this expression

Alternatively, manually calculate the norm of vector v.

Click to copy this expression

<region id="ID0E2ITDB" top="1632.0000000000002" left="38.400000000000006" actualWidth="207.04933364629747" actualHeight="36.780453040075308" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="82">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">N</id>
      <eval>
        <apply>
          <nthRoot />
          <placeholder />
          <apply>
            <plus />
            <apply>
              <plus />
              <apply>
                <pow />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
                <real>2</real>
              </apply>
              <apply>
                <pow />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
                <real>2</real>
              </apply>
            </apply>
            <apply>
              <pow />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
              </id>
              <real>2</real>
            </apply>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>