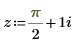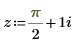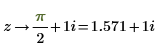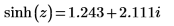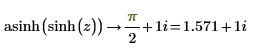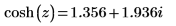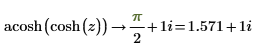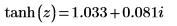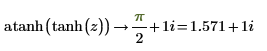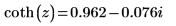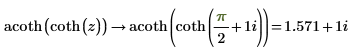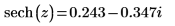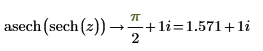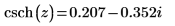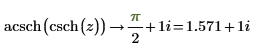Example: Hyperbolic and Inverse Hyperbolic Functions
Show that passing the evaluation result of a hyperbolic function to a corresponding inverse hyperbolic function returns the original input argument.
1. Define and evaluate the input argument z symbolically and numerically:
2. Evaluate sinh and pass the result to asinh then evaluate it symbolically and numerically:
As expected, both symbolic and numeric results are equal to the value of z.
3. Repeat the previous step using functions cosh and acosh:
4. Repeat the previous step using functions tanh and atanh:
5. Repeat the previous step using functions coth and acoth:
6. Repeat the previous step using functions sech and asech:
7. Repeat the previous step using functions csch and acsch: