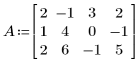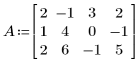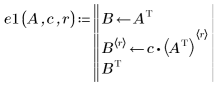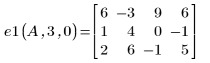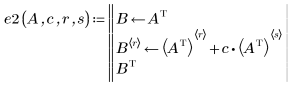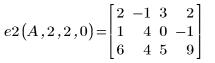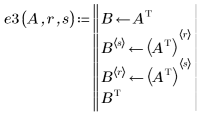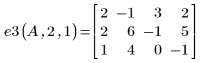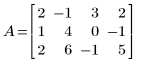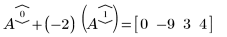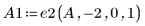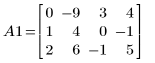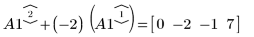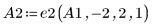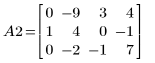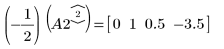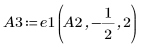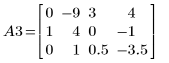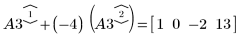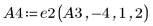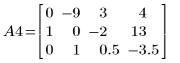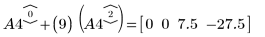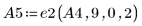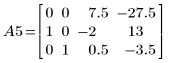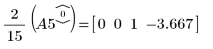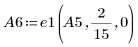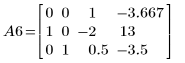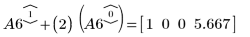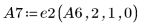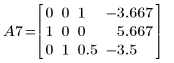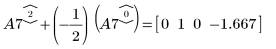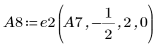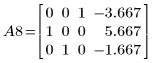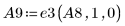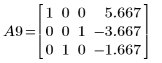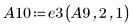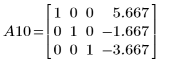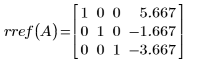Vectors, Matrices, and Tables > Creating Arrays and Tables > Example: Elementary Row Operations on Matrices
  
Example: Elementary Row Operations on Matrices
Perform three types of elementary row operations on an m x n matrix and show that there is a connection with the row-reduced echelon form.
1. Define an input matrix:
Click to copy this expression
2. Multiply row r by a scalar c:
Click to copy this expression
Click to copy this expression
3. Replace row r by row r plus c times row s:
Click to copy this expression
Click to copy this expression
4. Interchange rows r and s:
Click to copy this expression
Click to copy this expression
The row-reduced echelon form (rref) of a matrix
The row-reduced echelon form is an important technique used for solving a system of linear equations.
Utilize the following sequence of e1, e2, and e3 operations to find the row-reduced echelon form (rref) of matrix A:
1. Define matrix A
Click to copy this expression
2. Use e2 to replace row 0 of A by row 0 plus (-2) times row 1:
Click to copy this expression
Click to copy this expression
Click to copy this expression
3. Use e2 to replace row 2 of A1 by row 2 plus (-2) times row 1:
Click to copy this expression
Click to copy this expression
Click to copy this expression
4. Use e1 to multiply row 2 of A2 by (-1/2):
Click to copy this expression
Click to copy this expression
Click to copy this expression
5. Use e2 to replace row 1 of A3 by row 1 plus (-4) times row 2:
Click to copy this expression
Click to copy this expression
Click to copy this expression
6. Use e2 to replace row 0 of A4 by row 0 plus (9) times row 2:
Click to copy this expression
Click to copy this expression
Click to copy this expression
7. Use e1 to multiply row 0 of A5 by 2/15:
Click to copy this expression
Click to copy this expression
Click to copy this expression
8. Use e2 to replace row 1 of A6 by row 1 plus (2) times row 0:
Click to copy this expression
Click to copy this expression
Click to copy this expression
9. Use e2 to replace row 2 of A7 by row 2 plus (-1/2) times row 0:
Click to copy this expression
Click to copy this expression
Click to copy this expression
10. Use e3 to interchange rows 0 and 1 of A8:
Click to copy this expression
Click to copy this expression
11. Use e3 to interchange rows 1 and 2 of A9:
Click to copy this expression
Click to copy this expression
In this example, the above sequence of elementary row operations gives the row-reduced echelon form of matrix A.
12. Use the rref function to find the row-reduced echelon form of matrix A.
Click to copy this expression
The returned matrix is identical to matrix A10.