Ein besonderes Problem beim Zeichnen in der Perspektive stellen Kreise und Kreisbögen dar. Sie ändern mit dem veränderten Blickwinkel nicht nur ihre Größe wie die Linien, sondern auch ihre Form - sie werden zu Ellipsen.

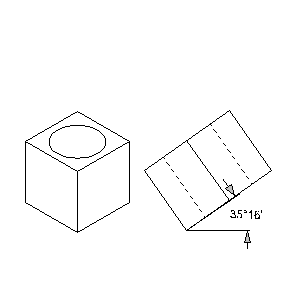
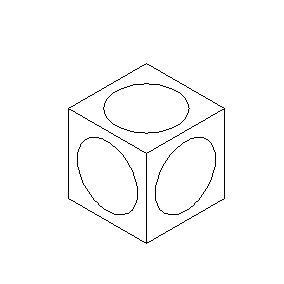
Es stellt sich die Frage, welche Ellipse benutzt werden muss, um einen Kreis in der Isometrie richtig abzubilden. Betrachten wir dazu den bekannten Würfel noch einmal. In der isometrischen Abbildung links wurde ein passender Kreis auf der Oberfläche hinzugefügt. Rechts sehen Sie noch mal den gekippten Würfel von der Seite.

 

Wie Sie sehen, ist die Fläche, auf der der Kreis liegt, um 35°16’ geneigt, wie bereits oben erwähnt. Die Neigung, auch Öffnungswinkel genannt, dient jetzt dazu, die Ellipse zu bestimmen, die benutzt werden soll. Besitzt eine Ellipse einen Öffnungswinkel von 35°16’, abgekürzt 35°, bedeutet dies, dass sie auf einer Fläche liegt, die um diesen Winkel zum Betrachter hin geneigt ist.

 

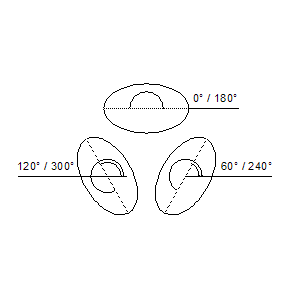
Ein weiterer wichtiger Begriff ist der Orientierungswinkel. Wie Sie in der Abbildung sehen, werden die Ellipsen auf den Seiten des Würfels gedreht dargestellt. Dabei ist der Öffnungswinkel in allen drei isometrischen Hauptachsen gleich, nur die Lage hat sich verändert. Die Lage einer Ellipse wird über den Orientierungswinkel definiert. Der Orientierungswinkel gibt die Neigung des Ellipsendurchmessers zur horizontalen Achse an.

 

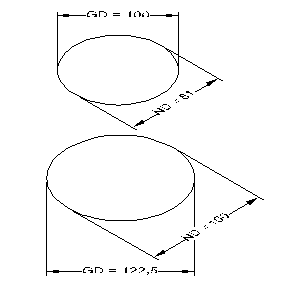
Auch bei Kreisen wird die perspektivische Verkürzung angewendet. Ein Kreis mit einem Durchmesser von 100 mm wird zu einer Ellipse mit dem gleichen Durchmesser. Dieser große Durchmesser (GD) wird auf der langen Achse der Ellipse abgetragen. Bei der perspektivischen Verkürzung hatten wir festgestellt, dass der Verkürzungsfaktor in den isometrischen Hauptachsen 81 % beträgt. Entsprechend wird der Durchmesser auf der Ellipse, in den Hauptachsen gemessen, ebenso verkürzt. Diesen Durchmesser nennen wir Nenndurchmesser (ND). In der Abbildung sehen Sie oben die Ellipse mit Verkürzung, darunter die Ellipse ohne Verkürzung.

In Arbortext IsoDraw können Sie den passenden Öffnungswinkel aus einem Popup-Menü auswählen. Der eingestellte Winkel wird auf alle anschließend gezeichneten Ellipsen angewendet.

Mit der Funktion Gitterausrichtung für die Hauptachsen wird die Ellipse beim Zeichnen in eine Hauptachse gezwungen. Mit der Mausbewegung wird die Ellipse auf die gewünschte Hauptachse gebracht. Damit ist automatisch der passende Lagewinkel der Ellipse gewährleistet.

Die isometrische Verkürzung gilt in Arbortext IsoDraw auch für Ellipsen, wie oben beschrieben. Sie können mit automatischer Verkürzung oder ohne Verkürzung arbeiten. Natürlich muss für alle Elemente dieselbe Option verwendet werden.