Circles and arcs pose a particular problem when drawing in perspective. When the perspective is altered, they change in terms of both length (as lines do) and shape – they become ellipses.

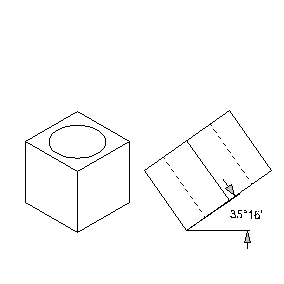
This raises the question as to what ellipse should be used in order to correctly depict a circle in an isometric representation. Let’s take another look at the cube. In the isometric figure on the left, a circle has been added to the top. On the right you can see the tipped cube again, viewed from the side.

 

As you can see, the area with the circle has been tilted by 35°16’ as explained above. The tilt, also known as the ellipse value, now serves to determine the ellipse that is to be used. If an ellipse has an ellipse value of 35°16’, or 35° for short, this means that it is positioned on a surface that is tilted by this angle towards the observer.

 

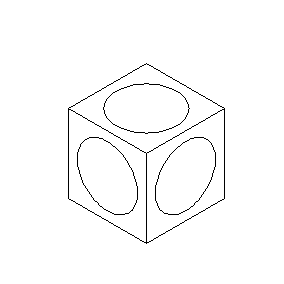
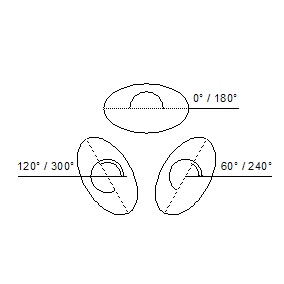
Another important factor is the orientation angle. As you can see in the figure, the ellipses on the sides of the cube are depicted as if they are rotated. The ellipse value is identical in all three major isometric axes, only the orientation has changed. The orientation of an ellipse is defined by the orientation angle. The orientation angle indicates the inclination of the ellipse diameter relative to the horizontal axis.

 

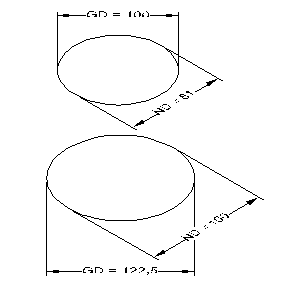
Perspective foreshortening is also applied to circles. A circle with a diameter of 100 mm becomes an ellipse with the same diameter. This large diameter (GD) is plotted on the long axis of the ellipse. When we looked at perspective foreshortening, we established that the foreshortening factor in the major isometric axes is 81%. The diameter of the ellipse, measured in the major axes, is also foreshortened by this factor. This diameter is known as the foreshortened diameter (ND). The figure shows the top ellipse with foreshortening and the bottom ellipse without foreshortening.

In Arbortext IsoDraw, you can select the appropriate ellipse value from a pop-up menu. The selected value is then applied to all the ellipses that are drawn subsequently.

The Grid Alignment function for the major axes forces the ellipse into a major axis as it is drawn. The ellipse can be moved to the desired major axis using the mouse. This automatically ensures that the appropriate ellipse value is used.

In Arbortext IsoDraw, isometric foreshortening also applies to ellipses, as described above. You can work with automatic foreshortening, or without foreshortening. However, the same option must naturally be used for all elements.