Verification Cases for Creo Simulation Live—Modal Analyses
Cantilever Beam Modal Analysis
Problem Statement: Consider a cantilever beam of length l and a width w and height h. Compute the first three bending modes and natural frequencies. (Note that the simulation results include orthogonal bending, torsional and axial modes. The results comparison compares the first three bending modes from a closed form solution with the equivalent simulation results.)
References: W. T. Thompson, Theory of Vibration with Applications, 2nd Edition, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1981, pg. 220
Material Properties | Geometric Properties |
Young’s modulus E= 70e9 Pa Poisson’s ratio ν = 0.35 Density ⍴ = 2700 kg/m^3 | l = 4 m w = 0.346 m h = 0.346 m |
Result Comparison—Simulation quality slider at default position
Results | Target | Creo Simulate | ANSYS Discovery Live | Creo Simulation Live | Percent Error |
Frequency Mode 1 (Hz) | 17.8 | 17.88 | 17.8 | 17.82 | 0.1 |
Frequency Mode 3 (Hz) | 111.5 | 110.03 | 108 | 107.98 | 3.2 |
Frequency Mode 6 (Hz) | 312.1 | 320.22 | 287.8 | 288.09 | 7.7 |
Simply-Supported Beam Modal Analysis
Problem Statement: To determine the fundamental frequency of a simply-supported beam of length 80 in. and uniform cross-section A = 4 in2 as shown below.
References: W. T. Thompson, Vibration Theory and Applications, 2nd Printing, Prentice-Hall, Inc.,Englewood Cliffs, NJ, 1965, pg. 18, ex. 1.5-1
Material Properties | Geometric Properties |
Young’s modulus E = 3e7 psi Poisson’s ratio ν = 0.3 Density ⍴= 0.2836 lb/in^3 | l = 80 in w = 2 in h = 2 in |
Result Comparison—Simulation quality slider at default position
(Simple support approximated by constraining 0.125 in imprinted faces.)
Results | Target | Creo Simulate | ANSYS Discovery Live | Creo Simulation Live | Percent Error |
Frequency Mode 1 (Hz) | 28.766 | 28.67 | 33.1 | 34.20 | 18.9 |
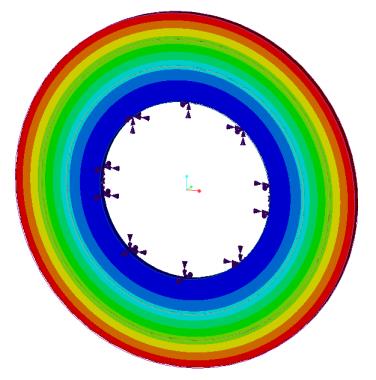
Modal Analysis of an Annular Plate
Problem Statement: An assembly of three annular plates has cylindrical support (fixed in the radial, tangential, and axial directions) applied on the cylindrical surface of the hole. Determine the first six natural frequencies.
References: R. J. Blevins, Formula for Natural Frequency and Mode Shape, Van Nostrand Reinhold Company Inc., 1979, Table 11-2, Case 4, pg. 247
Material Properties | Geometric Properties |
Young’s modulus E = 2.9008e7 psi Poisson’s ratio ν= 0.3 Density ⍴ = 0.28383 lb/in^3 | Inner diameter of inner plate = 20 in. Inner diameter of middle plate = 28 in Inner diameter of outer plate = 34 in Outer diameter of outer plate = 40 in Thickness of all plates = 1 in |
Result Comparison—Simulation quality slider at default position
Results | Target | Creo Simulate | ANSYS Discovery Live | Creo Simulation Live | Percent Error |
Frequency Mode 1 (Hz) | 310.9 | 310.92 | 321 | 321.1 | 3.27 |
Frequency Mode 2 (Hz) | 318.1 | 316.37 | 326.6 | 326.7 | 2.70 |
Frequency Mode 3 (Hz) | 318.1 | 316.50 | 326.7 | 326.7 | 2.70 |
Frequency Mode 4 (Hz) | 351.6 | 347.80 | 358 | 358.1 | 1.84 |
Frequency Mode 5 (Hz) | 351.6 | 347.94 | 358.1 | 358.2 | 1.88 |
Frequency Mode 6 (Hz) | 442.4 | 436.54 | 446.5 | 446.5 | 0.93 |
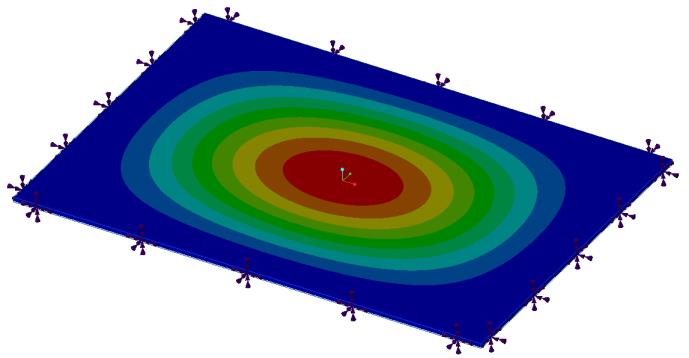
Modal Analysis of a Rectangular Plate
Problem Statement: Consider a rectangular plate with fixed supports where the dimensions of the plate are length = 6 in, width = 4 in and thickness = 0.063 in. Determine the natural frequency and mode shape.
References: R. Blevins, Formula for Natural Frequency and Mode Shape, Van Nostrand Reinhold Company Inc., 1979, Table 11-6
Material Properties | Geometric Properties |
Young’s modulus E = 1.0e7 psi Poisson’s ratio ν = 0.33 Density ⍴ = 0.1 lbm/in^3 | Length = 6 in Width = 4 in Thickness = 0.063 in |
Result Comparison—Simulation quality slider at default position
Results | Target | Creo Simulate | ANSYS Discovery Live | Creo Simulation Live | Percent Error |
Frequency Mode 1 (Hz) | 1016 | 1019.35 | 1075.7 | 1075.7 | 5.88 |