
|
Analysis Type:
|
Dynamic Frequency
|
|
Model Type:
|
3D
|
|
Comparison:
|
ANSYS No. 90
|
|
Reference:
|
Thomson, W. T. Vibration Theory and Applications. Prentice-Hall, Inc., Englewood Cliffs, N. J., 2nd Printing, 1965.
|
|
Description:
|
Determine the response of the two-mass-spring system when excited by a harmonic force acting on mass at point B.
|

Element Type: | mass (2), spring (3) | ||
Units: | IPS | ||
Dimensions: | spring length: 1 (arbitrary) | ||
Mass Properties: | |||
M: 0.5 | Mxx: 0 | Mxy: 0 | Mxz: 0 |
Myy: 0 | Myz: 0 | Mzz: 0 | |
Spring Properties: (extensional stiffness) | |||
Kxx: 200 | Kxy: 0 | Kxz: 0 | |
Kyy: 0 | Kyz: 0 | Kzz: 0 | |
Constraints: | Location: | Degrees of Freedom: |
constraint1 | placed on points A and D placed on points B and C | fixed in all DOF fixed in all DOF except TransX |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation: |
load1 | placed on point B: FX = 200 | N/A | N/A |
Loc | Theory | ANSYS | Structure1 | % Diff | |
Frequency = 1.5 Hz Disp/phase at B, C (m=dispx_2, 3/ phase_2, 3) | point B | 0.8227/0 | 0.8227/0 | 0.8227/0 | 0% |
point C | 0.4627/0 | 0.4627/0 | 0.4627/0 | 0% | |
Frequency = 4.0 Hz Disp/phase at A, B (m=dispx_2, 3/ phase_2, 3) | point B | 0.5115/ 180 | 0.5115/ 180 | 0.5115/180 | 0% |
point C | 1.2153/ 180 | 1.2153/ 180 | 1.215/180 | 0% | |
Frequency = 6.5Hz Disp/phase at A, B (m=dispx_2, 3/ phase_2, 3) | point B | 0.5851/ 180 | 0.5851/ 180 | 0.5851/180 | 0% |
point C | 0.2697/0 | 0.2697/0 | 0.2697/0 | 0% | |
Convergence %: 0% on Frequency & Local Disp | Max P: 1 | No. Equations: 2 | |||
Analysis Type: | Dynamic Frequency |
Model Type: | Beam |
Comparison: | NAFEMS Benchmark |
Reference: | Selected Benchmarks for Forced Vibration, Report No. E1261/R002 Issue 03.2/9 February 1989 , pp. 17. Test 5H |
Description: | Determine response of simple supported square section beam when excited by Harmonic force uniformly distributed over beam. |
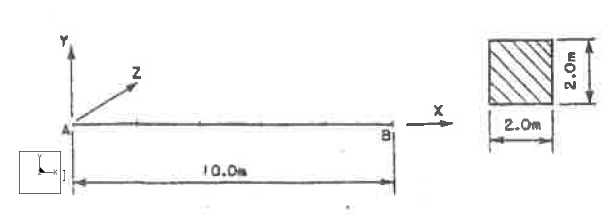
Element Type: | Square Beam | |
Units: | MKS | |
Dimensions: | L: 10.0, a =2 | |
Material Properties: | Mass Density: 8000 Young's Modulus: 2e11 | Poisson's Ratio: 0.3 |
Constraints: | Location: | Degrees of Freedom: |
Placed on point A Placed on point B : | Fixed in TransX, TransY, TransZ and Rotation Rx Fixed in TransY and TransZ |
Loads | Details |
Force Fy = 1e6 N/m, damping = 2 % in all 16 modes used, frequency range 0 to 60 Hz |
NAFEMS | Structure | % Diff | |
Peak Displacement at mid-span (mm)) | 13.45 | 13.5129 | 0.467 |
Frequency (Hz) | 42.65 | 42.6002 | 0.116 |
Analysis Type: | Dynamic Frequency |
Model Type: | 3D |
Comparison: | NAFEMS Benchmark |
Reference: | Selected Benchmarks for Forced Vibration, Report No. E1261/R002 Issue 03./ 9 th February 1989, pp 23. Test 13H |
Description: | Determine response of simple supported thin square plate when excited by Harmonic force uniformly distributed over plate. |
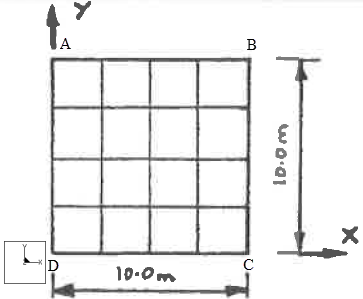
Element Type: | Shell | |
Units: | MKS | |
Dimensions: | L: 10.0, thickness: 0.05 | |
Material Properties: | Mass Density: 8000 Young's Modulus: 2e11 | Poisson's Ratio: 0.3 |
Constraints: | Location: | Degrees of Freedom: |
Placed on edges AD and BC : Placed on edges AB and DC : | fixed in TransY, TransZ , RotX, and RotZ fixed in TransX, TransZ , RotY, and RotZ |
Loads | Details |
Force Fy = 100 Pa , damping = 2 % in all 16 modes used, frequency range 0 to 4.16 Hz |
NAFEMS | Structure | % Diff | |
Peak Displacement at centre of plate (mm) | 45.42 | 45.4466 | 0.0585 |
Frequency (Hz) | 2.377 | 2.37603 | 0.0408 |