|
Analysis Type:
|
Modal
|
|
Model Type:
|
2D Plane Strain
|
|
Comparison:
|
Theoretical Results
|
|
Reference:
|
Roark, R.J. and Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co. 1982. pp.576578.
|
|
Description:
|
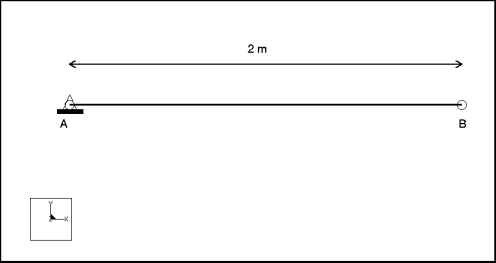
Find the fundamental frequency of a cantilever plate modeled as a plane strain model.
|

Element Type: | 2D shell (1) | |
Units: | MKS | |
Dimensions: | width: 2 thickness: 0.01 | |
Material Properties: | Mass Density: 7850 Cost Per Unit Mass: 0 Young's Modulus: 2e11 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on point A: fixed in all DOF | |
Theory | Structure | % Difference | |
Fundamental Frequency (Hz) (mode=1) | 2.1393 | 2.1374 | 0.08% |
Convergence %: 0.4% on Frequency | Max P: 4 | No. Equations: 12 | |
Analysis Type: | Modal |
Model Type: | 2D Plane Stress |
Comparison: | Theoretical Results |
Reference: | Roark, R.J. and Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co. 1982. pp.576578. |
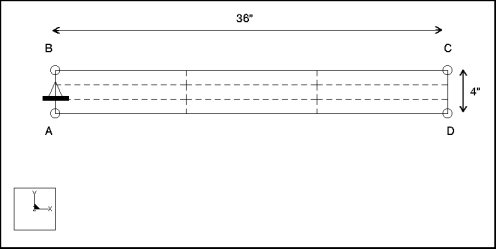
Description: | Find the fundamental frequency for the lateral vibration of a cantilever plate. |
Element Type: | 2D plate (1) | |
Units: | IPS | |
Dimensions: | length: 36 width: 4 thickness: 0.1 | |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on edge A-B: fixed in TransX and TransY | |
Theory | Structure | % Difference | |
Fundamental Frequency (Hz) (mode=1) | 101.326 | 100.988 | 0.33% |
Convergence %: 0.4% on Frequency | Max P: 6 | No. Equations: 42 | |
Analysis Type: | Modal |
Model Type: | 2D Plane Strain |
Comparison: | Theoretical Results |
Reference: | Roark, R.J., and Young, W.C. Formulas for Stress and Strain, NY: McGraw-Hill Book Co. 1982. pp.576578. |
Description: | Find the fundamental frequency of a cantilever plate modeled as a plane strain model. |
Element Type: | 2D solid (2) | |
Units: | IPS | |
Dimensions: | length: 36 width: 4 | |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on edge A-B: fixed in TransX, TransY, and RotZ | |
Theory | Structure | % Difference | |
Fundamental Frequency (Hz) (mode=1) | 106.219 | 106.604 | 0.36% |
Convergence %: 0.8% on Frequency | Max P: 6 | No. Equations: 42 | |
Analysis Type: | Modal |
Model Type: | 2D Axisymmetric |
Comparison: | ANSYS No. 67 |
Reference: | Timoshenko, S., and Young, D.H. Vibration Problems in Engineering. 3rd ed. NY: D. Van Nostrand Co., Inc. 1955. p. 425, Art. 68. |
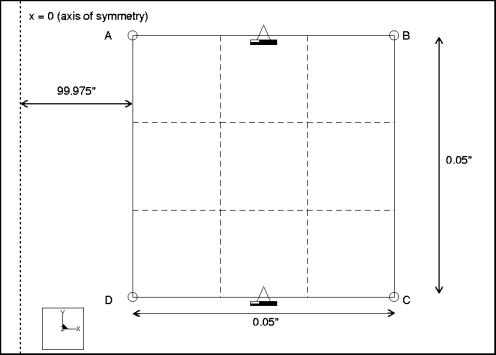
Description: | Find the fundamental frequency for the radial vibration of an annulus modeled axisymmetrically. |
Element Type: | 2D solid (1) | |
Units: | IPS | |
Dimensions: | inner radius: 99.975 outer radius: 100.025 height: 0.05 | |
Material Properties: | Mass Density: 7.3e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on edge A-B: fixed in TransY and RotZ placed on edge C-D: fixed in TransY and Rot Z | |
Theory | ANSYS | Structure | % Difference | |
Radial Frequency (Hz) (mode=1) | 322.64 | 322.64 | 322.64 | 0.0% |
Convergence %: 0.0% on Frequency | Max P: 2 | No. Equations: 10 | ||
Analysis Type: | Modal |
Model Type: | 3D |
Comparison: | Theoretical Results |
Reference: | Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity. 4th ed. NY: Dover Publications. 1944. p. 452, Art. 293b. |
Description: | Determine the first and second modal frequencies for the radial vibration of a ring modeled as a one-quarter model. |
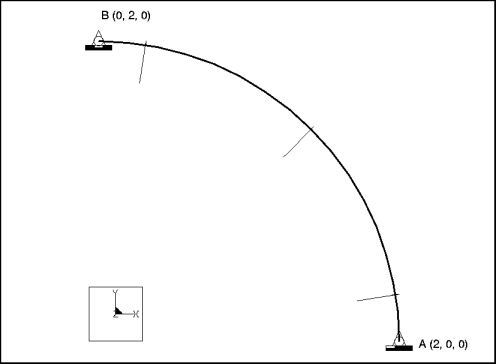
Element Type: | beam (1) | |
Units: | IPS | |
Dimensions: | radius: 2 | |
Beam Properties: | Area: 0.01 IYY: 1e3 Shear FY: 0.83333 CY: 1 | J: 1.008e3 IZZ: 8.33e6 Shear FZ: 0.83333 CZ: 1 |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF except TransX placed on point B: fixed in all DOF except TransY | |
Theory | Structure | % Difference | |
Mode 1 Frequency (Hz) | 625.65 | 624.43 | 0.19% |
Mode 2 Frequency (Hz) | 3393.06 | 3369.13 | 0.70% |
Convergence %: 0.0% on Frequency | Max P: 9 | No. Equations: 50 | |
Analysis Type: | Modal |
Model Type: | 3D |
Comparison: | ANSYS No. 62 |
Reference: | Timoshenko, S., and Young, D.H. Vibration Problems in Engineering. 3rd ed. NY: D. Van Nostrand Co., Inc. 1955. p. 392, Art. 62. |
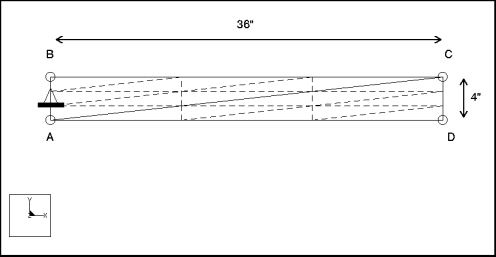
Description: | Find the fundamental frequency for the lateral vibration of a cantilever, wedge-shaped plate. |
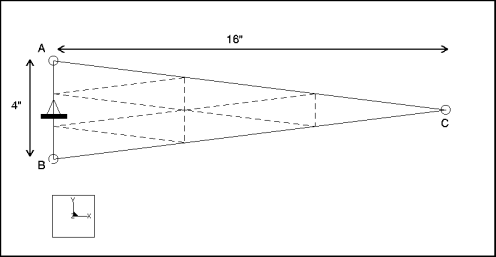
Element Type: | shell (1) | |
Units: | IPS | |
Dimensions: | length: 16 width: 4 thickness: 1 | |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on edge A-B: fixed in all DOF | |
Theory | ANSYS | Structure | % Difference | |
Frequency (Hz) (mode=1) | 259.16 | 260.99 | 259.15 | 0.004% |
Convergence %: 0.0% on Frequency | Max P: 4 | No. Equations: 60 | ||
Analysis Type: | Modal |
Model Type: | 3D |
Comparison: | Theoretical results |
Reference: | Roark, R.J., and Young, W.C. Formula for Stress and Strain. NY: McGraw-Hill Co. 1982. p.576. |
Description: | A cantilever cylindrical shell is modeled as a half cylinder using symmetry. Find the fundamental frequency. |
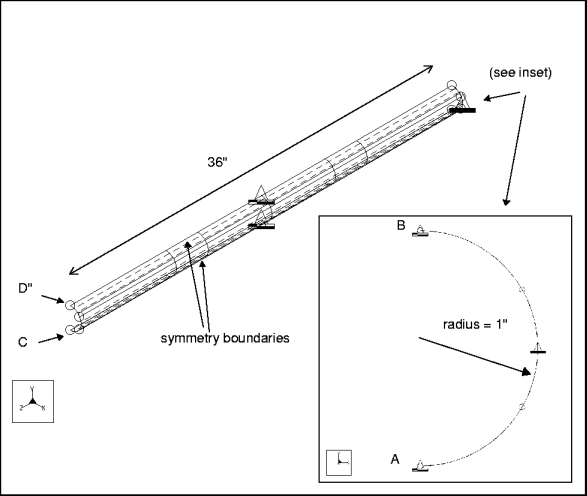
Element Type: | shell (3) | |
Units: | IPS | |
Dimensions: | length: 36 radius: 1 thickness: 0.1 | |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on edge A-B: fixed in all DOF placed on edge A-C, B-D: fixed in TransX, RotY, and RotZ | |
Theory | Structure | % Difference | |
Frequency (Hz) (mode=1) | 62.05 | 62.125 | 0.12% |
Convergence %: 0.4% on Frequency | Max P: 6 | No. Equations: 180 | |
Analysis Type: | Modal |
Model Type: | 3D |
Comparison: | ANSYS No. 62 |
Reference: | Timoshenko, S., and Young, D.H. Vibration Problems in Engineering. 3rd ed. NY: D. Van Nostrand Co., Inc. 1955. p. 392, Art. 62. |
Description: | Find the fundamental frequency for the lateral vibration of a cantilever, wedge-shaped plate. |
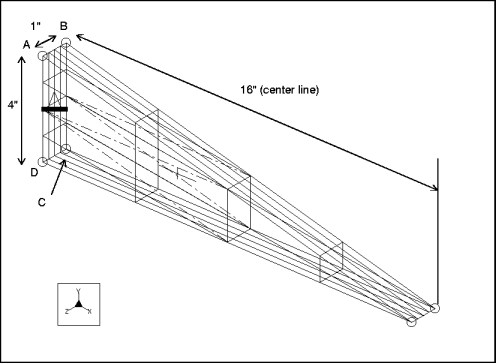
Element Type: | solid (1) | |
Units: | IPS | |
Dimensions: | length: 16 width: 4 depth: 1 | |
Material Properties: | Mass Density: 7.28e–4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on face A-B-C-D: fixed in all DOF | |
Theory | ANSYS | Structure | % Difference | |
Fundamental Frequency (Hz) (mode=1) | 259.16 | 260.99 | 259.24 | 0.03% |
Convergence %: 0.0% on Frequency | Max P: 4 | No. Equations: 72 | ||
Analysis Type: | Modal |
Model Type: | 3D |
Reference: | NAFEMS, SBNFA (November 1987), Test 1. |
Description: | Determine the first to eighth modal frequencies for the in-plane vibration of a cross with a pin joint at points A, B, C, & D. |
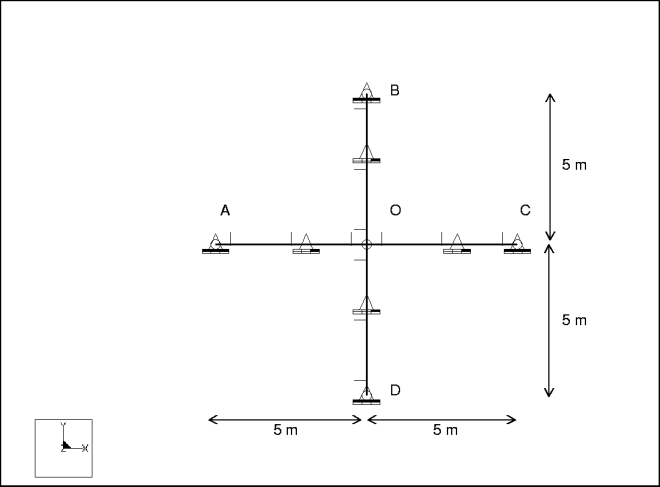
Element Type: | beam (4) | |
Units: | NMS | |
Dimensions: | length: 5 | |
Beam Properties: | Area: 0.015625 IYY: 2.0345e–5 Shear FY: 0.83333 CY: 0.0625 | J: 4.069e–5 IZZ: 2.0345e–5 Shear FZ: 0.83333 CZ: 0.0625 |
Material Properties: | Mass Density: 8000 Cost Per Unit Mass: 0 Young's Modulus: 2e11 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on points A, B, C, D: fixed TransX, TransY, TransZ placed on beams A-O, B-O, C-O, D-O: fixed in TransZ | |
Theory | Structure | % Difference | |
Mode 1 Frequency (Hz) | 11.336 | 11.312 | 0.211% |
Mode 2 & 3 Frequency (Hz) | 17.709 | 17.636 | 0.412% |
Mode 4 Frequency (Hz) | 17.709 | 17.636 | 0.412% |
Mode 5 Frequency (Hz) | 45.345 | 45.155 | 0.419% |
Mode 6 & 7 Frequency (Hz) | 57.390 | 56.692 | 1.216% |
Mode 8 Frequency (Hz) | 57.390 | 57.001 | 0.677% |
Convergence %: 3.4% on Frequency | Max P: 8 | No. Equations: 157 | |
Analysis Type: | Modal |
Model Type: | 3D |
Reference: | NAFEMS, SBNFA (November 1987), Test 53. |
Description: | Determine the first to fifth modal frequencies for the axisymmetric vibration of an annular plate. |
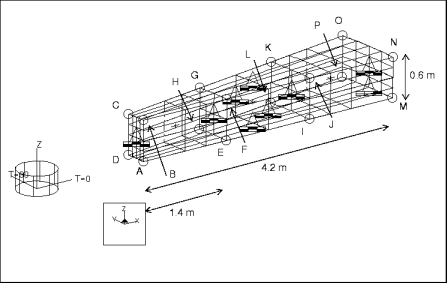
Element Type: | solid (3) | |
Units: | NMS | |
Dimensions: | inner radius: 1.8 outer radius: 6 height: 0.6 | |
Material Properties: | Mass Density: 8000 Cost Per Unit Mass: 0 Young's Modulus: 2e11 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | Location | Degrees of Freedom |
constraint1 | placed on surfaces ABCD, BCNO, ADMP, ABMN, CDPO, MNOP | fixed in TransT, RotR, and RotZ |
placed on curve MP | fixed in TransZ |
Theory | Structure | % Difference | |
Modal 1 Frequency (Hz) | 18.583 | 18.550 | 0.17% |
Modal 2 Frequency (Hz) | 140.15 | 138.22 | 1.37% |
Modal 3 Frequency (Hz) | 224.16 | 224.16 | 0% |
Modal 4 Frequency (Hz) | 358.29 | 355.80 | 0.7% |
Modal 5 Frequency (Hz) | 629.19 | 620.43 | 1.4% |
Convergence %: 1.3 on Frequency | Max P: 9 | No. Equations: 1094 | |